| Ojogo | Como jogar | Minimax | Poda Alfa-Beta |
Reversi, também conhecido como Othello é um jogo cuja história ninguém sabe ao certo. É um jogo que utiliza um tabuleiro de 8 x 8 casas para dois jogadores com peças em forma de discos com um lado preto e outro branco que podem ser viradas no decorrer do jogo.
Alguns acreditam que o jogo tenha sido inventado na China com o nome de Fan Mian. Outros crêem que foi criado em Londres por John W. Mollett ou por Lewis Waterman no séc XIX.
O tabuleiro usado nos torneios internacionais vem do jogo Othello inventado pelo japonês Goro Hasegawa em 1971, inspirado no jogo de estratégia “Go”. Hasegawa procurou criar um jogo que era rico na estratégia, mas ainda acessível ao jogador casual e, obteve como resultado um jogo que difere do Reversi apenas na forma como se inicia a partida e no compartilhamento das peças entre os jogadores. Reversi / Othello embora seja um jogo fácil de aprender, não é necessariamente fácil dominar todas as nuances estratégicas proporcionadas, por isso os que querem se tornar “experts” neste jogo precisarão praticar e jogar continuamente, percorrendo um longo caminho, para aperfeiçoar a sua estratégia.
Caso tenha preguiça de ler, veja o video
No caso do tabuleiro real, é jogado entre 2 jogadores.
O objetivo do jogo é ter a maioria dos discos da sua cor com a face virada para cima no tabuleiro ao fim da partida.
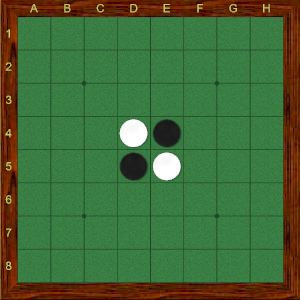
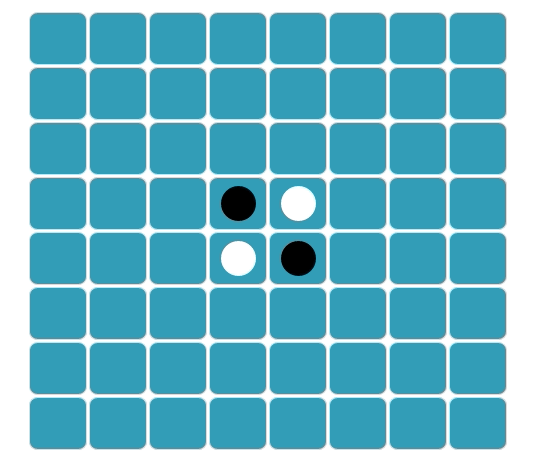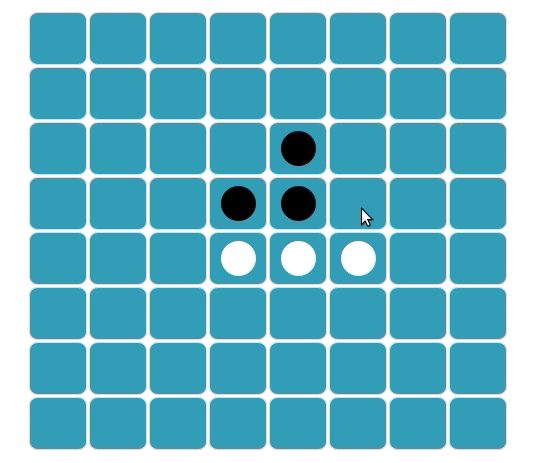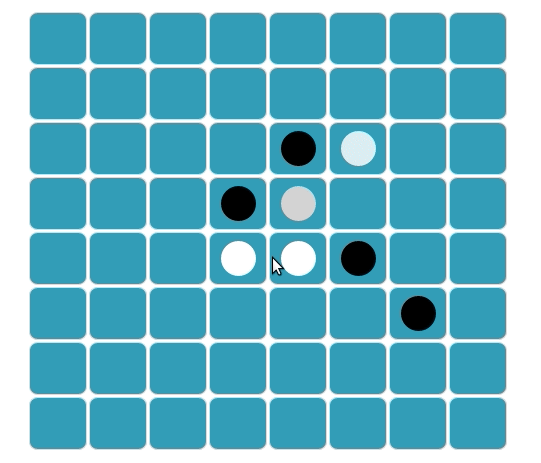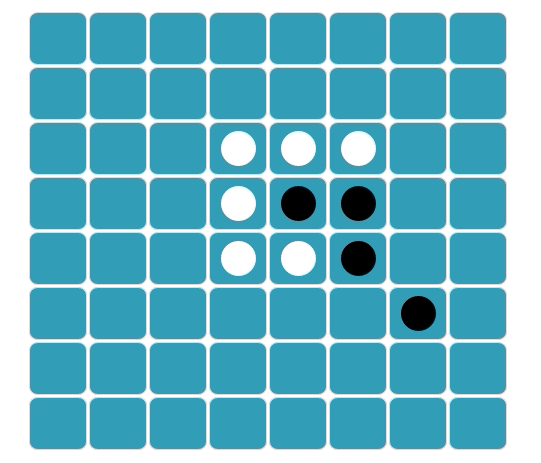
Cada jogador fica com 32 discos e escolhe uma cor para usar durante a partida. Nas posições do preto são colocados dois discos pretos e nas posições do branco, dois discos brancos como mostra a figura 1.
“Flanquear” significa posicionar um disco no tabuleiro de forma que a linha(ou linhas) de discos de seu oponente seja limitada em cada extremidade por um disco de sua cor. Uma linha pode ser formada por um ou mais discos.
Aqui está um exemplo: O disco branco A já foi posicionado no tabuleiro. A colocação do disco branco B flanqueia a linha de três discos pretos.
O Branco vira os discos flanqueados e a linha agora fica assim:
-
O Preto sempre faz o movimento primeiro.
-
Se um jogador não puder flanquear e virar ao menos um disco do oponente, ele perde a vez e seu oponente joga outra vez. Entretanto, se o lance é possível o jogador não pode passar sua vez.
-
Um disco pode flanquear vários discos em uma ou mais linhas em várias direções ao mesmo tempo – horizontal, vertical ou diagonal. Uma “linha” é definida como um ou mais discos em uma linha reta contínua.
-
Um jogador não pode passar por cima do disco de sua cor(s) para flanquear um disco oposto a ele.
-
O(s) disco(s) deve(m) ser flanqueados(s) como resultado direto de uma jogada sendo virado(s) na linha do disco posicionado.
-
Todos os discos flanqueados em qualquer movimento devem ser virados, mesmo que fosse uma vantagem para o jogador não virá-los.
-
Uma vez que um disco é colocado em um quadrado, ele nunca poderá ser movido para outro quadrado mais tarde no jogo.
-
Quando não há mais possibilidade de movimento para ambos os jogadores, o jogo termina. Os discos são contados e o jogador com a maioria dos discos da sua cor é o vencedor da partida.
- Nota: É possível que um jogo termine antes que de todas as 64 casa sejam preenchidas.
No caso desta implementação, o jogador humano (peças pretas) compete contra o computador
- Para realizar a busca do movimento realizado por meio de inteligência artificial, foi utilizado um algoritmo conhecido como MiniMax com poda alfa e beta
O algoritmo Mini-max é um algoritmo recursivo ou de retrocesso que é usado na tomada de decisões e na teoria dos jogos. Ele fornece um movimento ideal para o jogador, supondo que o oponente também esteja jogando de forma otimizada.
O algoritmo Mini-Max usa recursão para pesquisar na árvore do jogo.
O algoritmo Min-Max é usado principalmente para jogos em IA. Como xadrez, damas, jogo da velha, go e vários jogos de dois jogadores. Este algoritmo calcula a decisão minimax para o estado atual.
Neste algoritmo, dois jogadores jogam o jogo, um é denominado MAX e o outro é denominado MIN.
Ambos os jogadores lutam como o jogador adversário obtém o benefício mínimo enquanto eles obtêm o benefício máximo.
Ambos os jogadores do jogo são oponentes um do outro, onde MAX selecionará o valor maximizado e MIN selecionará o valor minimizado.
O algoritmo minimax executa um algoritmo de pesquisa em profundidade para a exploração de toda a árvore do jogo.
O algoritmo minimax segue todo o caminho até o nó terminal da árvore e, em seguida, retrocede a árvore conforme a recursão.
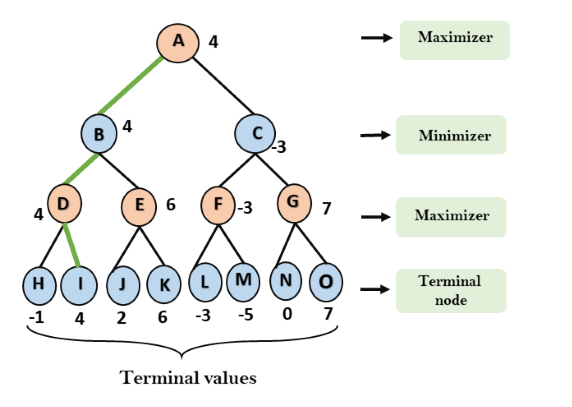
O funcionamento do algoritmo minimax pode ser facilmente descrito usando um exemplo. Abaixo, um exemplo de árvore de jogo que representa o jogo para dois jogadores.
Neste exemplo, existem dois jogadores, um é denominado Maximizer e o outro é denominado Minimizer.
O Maximizer tentará obter a pontuação máxima possível e o Minimizer tentará obter a pontuação mínima possível.
Este algoritmo aplica DFS, portanto, nesta árvore do jogo, temos que percorrer todo o caminho através das folhas para chegar aos nós terminais.
No nó terminal, os valores terminais são fornecidos, portanto, compararemos esses valores e retrocederemos na árvore até que ocorra o estado inicial. A seguir estão as principais etapas envolvidas na resolução da árvore do jogo para dois jogadores:
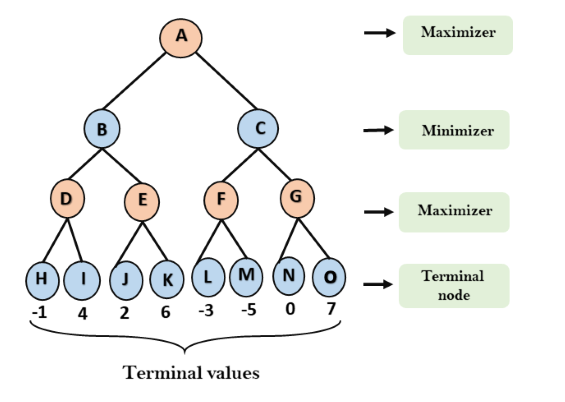
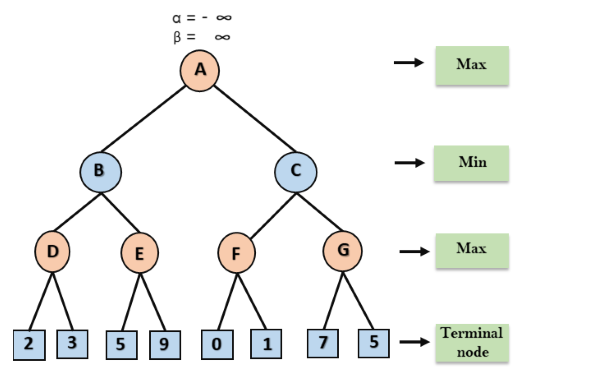
Etapa 1: Na primeira etapa, o algoritmo gera toda a árvore do jogo e aplica a função de utilidade para obter os valores de utilidade para os estados terminais. No diagrama de árvore abaixo, vamos considerar que A é o estado inicial da árvore. Suponha que o maximizador dê o primeiro turno, que tem o valor inicial do pior caso = - infinito, e o minimizador dê o próximo turno, que tem o valor inicial do pior caso = + infinito.
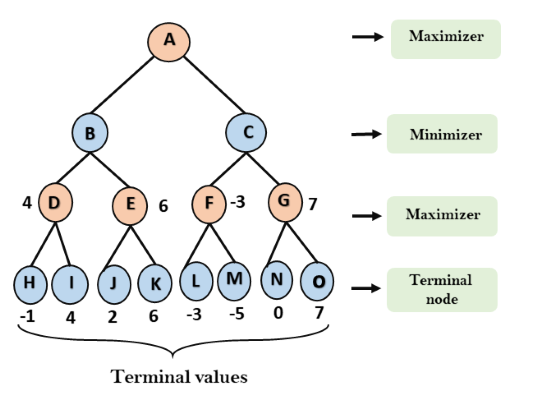
Passo 2: Agora, primeiro encontramos o valor dos utilitários para o Maximizer, seu valor inicial é -∞, então iremos comparar cada valor no estado terminal com o valor inicial do Maximizer e determinar os valores dos nós mais altos. Vai encontrar o máximo entre todos.
- Para o nó D max (-1, - -∞) => max (-1,4) = 4
- Para o Nó E max (2, -∞) => max (2, 6) = 6
- Para o nó F max (-3, -∞) => max (-3, -5) = -3
- Para o nó G max (0, -∞) = max (0, 7) = 7
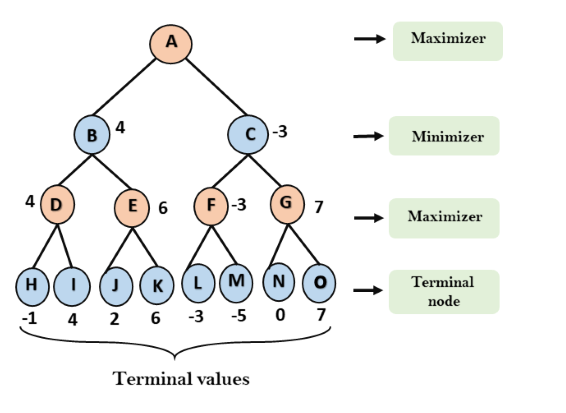
Etapa 3: Na próxima etapa, é a vez do minimizador, então ele irá comparar o valor de todos os nós com + ∞, e encontrará os valores dos nós da 3ª camada.
- Para o nó B = min (4,6) = 4
- Para o nó C = min (-3, 7) = -3
Etapa 4: agora é a vez do Maximizer e ele escolherá novamente o valor máximo de todos os nós e encontrará o valor máximo para o nó raiz. Nesta árvore de jogo, existem apenas 4 camadas, portanto, chegamos imediatamente ao nó raiz, mas em jogos reais, haverá mais de 4 camadas.
- Para o nó A max (4, -3) = 4
O algoritmo Complete -Min-Max está completo. Definitivamente encontrará uma solução (se houver), na árvore de pesquisa finita.
O algoritmo Ótimo -Mín-Máx é ótimo se ambos os oponentes estão jogando de maneira ideal.
Complexidade de tempo - como ele executa DFS para a árvore do jogo, então a complexidade de tempo do algoritmo Min-Max é O (b^m) , onde b é o fator de ramificação da árvore do jogo e m é a profundidade máxima da árvore.
Complexidade do espaço - A complexidade do espaço do algoritmo Mini-max também é semelhante ao DFS, que é O (bm) .
Limitação do algoritmo minimax: A principal desvantagem do algoritmo minimax é que ele fica muito lento para jogos complexos como xadrez, go, etc. Esse tipo de jogo tem um grande fator de ramificação, e o jogador tem muitas opções para decidir. Essa limitação do algoritmo minimax pode ser melhorada a partir da poda alfa-beta.
Como vimos no algoritmo de pesquisa minimax, o número de estados do jogo que ele deve examinar é exponencial na profundidade da árvore. Uma vez que não podemos eliminar o expoente, podemos cortá-lo pela metade. Portanto, existe uma técnica pela qual, sem verificar cada nó da árvore do jogo, podemos calcular a decisão correta do minimax, e essa técnica é chamada de poda . Isso envolve dois parâmetros de limite Alfa e beta para expansão futura, por isso é chamado de poda alfa-beta . É também chamado de Algoritmo Alfa-Beta .
A poda alfa-beta pode ser aplicada em qualquer profundidade de uma árvore e, às vezes, não apenas poda as folhas da árvore, mas também a subárvore inteira.
Os dois parâmetros podem ser definidos como:
Alpha: A melhor escolha (valor mais alto) que encontramos até agora em qualquer ponto ao longo do caminho do Maximizer. O valor inicial de alfa é -∞ .
Beta: a melhor escolha (valor mais baixo) que encontramos até agora em qualquer ponto ao longo do caminho do Minimizer. O valor inicial de beta é + ∞ .
A poda alfa-beta para um algoritmo minimax padrão retorna o mesmo movimento que o algoritmo padrão, mas remove todos os nós que não estão realmente afetando a decisão final, mas tornando o algoritmo lento. Conseqüentemente, ao podar esses nós, torna o algoritmo mais rápido.
A principal condição necessária para a poda alfa-beta é: ***α >= β ***
Pontos principais sobre a poda alfa-beta:
- O Max player só atualizará o valor de alfa.
- O jogador Min irá apenas atualizar o valor do beta.
- Durante o retrocesso da árvore, os valores dos nós serão passados para os nós superiores em vez dos valores de alfa e beta.
- Só passaremos os valores alfa e beta para os nós filhos.
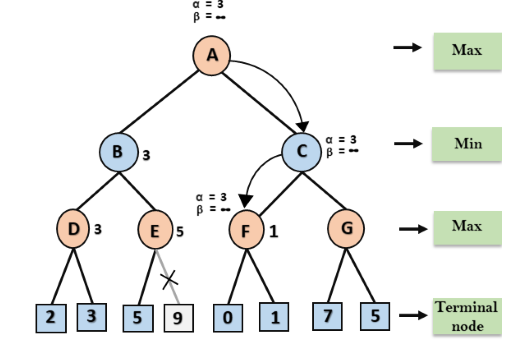
Etapa 1: Na primeira etapa, o jogador Max começará o primeiro movimento do nó A, onde α = -∞ e β = + ∞, esses valores de alfa e beta passados para o nó B onde novamente α = -∞ e β = + ∞, e o Nó B passa o mesmo valor para seu filho D.
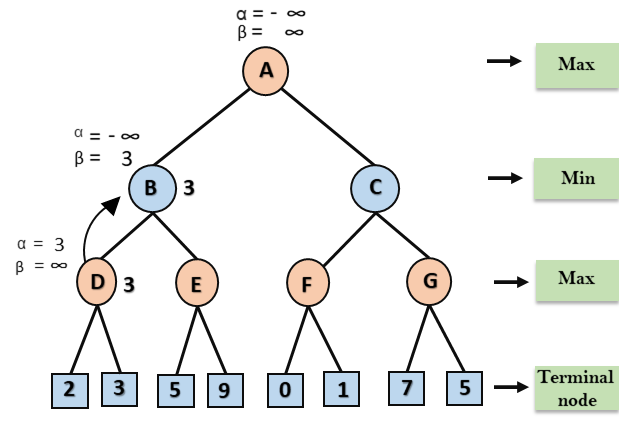
Etapa 2: No Nó D, o valor de α será calculado na sua vez para o máx. O valor de α é comparado primeiro com 2 e depois com 3, e o máximo (2, 3) = 3 será o valor de α no nó D e o valor do nó também será 3.
Etapa 3: Agora o algoritmo retrocede para o nó B, onde o valor de β mudará, pois esta é uma volta de Min, agora β = + ∞, irá comparar com o valor dos nós subsequentes disponíveis, ou seja, min (∞, 3) = 3, portanto, no nó B agora α = -∞ e β = 3.
Na próxima etapa, o algoritmo percorre o próximo sucessor do Nó B, que é o nó E, e os valores de α = -∞ e β = 3 também serão passados.
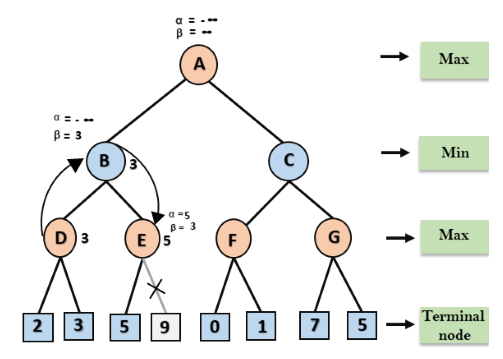
Etapa 4: no nó E, Max fará sua vez, e o valor de alfa mudará. O valor atual de alfa será comparado com 5, então max (-∞, 5) = 5, portanto, no nó E α = 5 e β = 3, onde α> = β, então o sucessor correto de E será podado, e o algoritmo não o percorrerá, e o valor no nó E será 5.
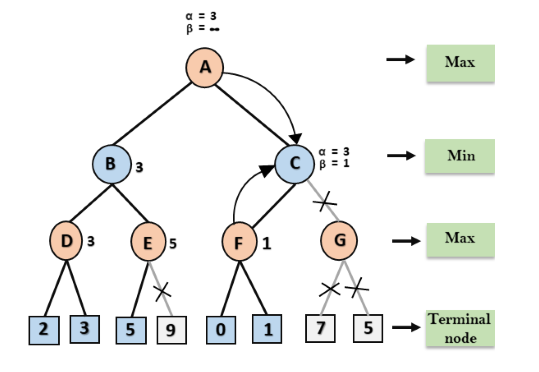
Etapa 5: Na próxima etapa, o algoritmo retrocede novamente a árvore, do nó B para o nó A. No nó A, o valor de alfa será alterado, o valor máximo disponível é 3, pois max (-∞, 3) = 3 e β = + ∞, esses dois valores agora passam para o sucessor direito de A, que é o Nó C.
No nó C, α = 3 e β = + ∞, e os mesmos valores serão repassados ao nó F.
Etapa 6: No nó F, novamente o valor de α será comparado com o filho esquerda que é 0, e max (3,0) = 3, e então comparado com o filho a direita que é 1, e max (3,1) = 3 ainda α permanece 3, mas o valor do nó de F se tornará 1.
Etapa 7: o nó F retorna o valor do nó 1 para o nó C, em C α = 3 e β = + ∞, aqui o valor de beta será alterado, ele será comparado com 1 então min (∞, 1) = 1. Agora em C, α = 3 e β = 1, e novamente satisfaz a condição α> = β, então o próximo filho de C que é G será podado, e o algoritmo não computará a subárvore inteira G.
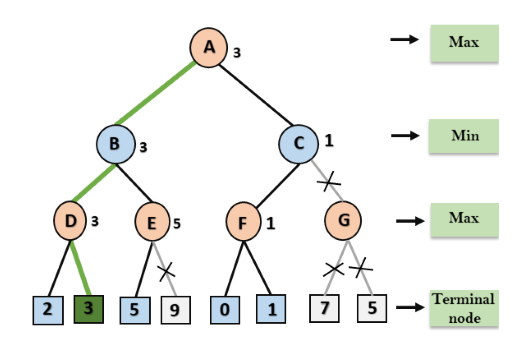
Etapa 8: C agora retorna o valor de 1 para A aqui o melhor valor para A é max (3, 1) = 3. A seguir está a árvore do jogo final que mostra os nós que são computados e os nós que nunca foram computados. Portanto, o valor ideal para o maximizador é 3 para este exemplo.
- história do jogo - Magazine Luiza
- Como jogar - Federação Brasileira de Othelo FBO
- Algoritmo Mini-Max em Inteligência Artificial
- Implementação do jogo foi baseado no trabalho de Jean Marcos Silva Santos Busca com Adversários - Usando o método de busca minimax para o jogo othelo - ICMC - USP São Carlos - 2020