|
| 1 | +--- |
| 2 | +title: '王树森推荐系统学习笔记_特征交叉' |
| 3 | +description: "" |
| 4 | +date: "2025-09-27" |
| 5 | +tags: |
| 6 | + - tag-one |
| 7 | +--- |
| 8 | + |
| 9 | +# 王树森推荐系统学习笔记_特征交叉 |
| 10 | + |
| 11 | +## 特征交叉 |
| 12 | + |
| 13 | +### Factorized Machine (FM) |
| 14 | + |
| 15 | +#### 线性模型 |
| 16 | + |
| 17 | +- 有 $d$ 个特征,记作 $ \mathbf{x} = [x_1, \cdots, x_d] $。 |
| 18 | + |
| 19 | +- **线性模型**: |
| 20 | + |
| 21 | + $$ |
| 22 | + p = b + \sum_{i=1}^{d} w_i x_i。 |
| 23 | + $$ |
| 24 | + |
| 25 | +- **模型有 $d + 1$ 个参数**:$ \mathbf{w} = [w_1, \cdots, w_d] $ 和 $b$。 |
| 26 | + |
| 27 | +- **预测是特征的加权和**。(*只有加,没有乘。*) |
| 28 | + |
| 29 | +#### 二阶交叉特征 |
| 30 | + |
| 31 | +- **有 $d$ 个特征,记作** $ \mathbf{x} = [x_1, \cdots, x_d] $。 |
| 32 | + |
| 33 | +- **线性模型 + 二阶交叉特征**: |
| 34 | + |
| 35 | + $$ |
| 36 | + p = b + \sum_{i=1}^{d} w_i x_i + \sum_{i=1}^{d} \sum_{j=i+1}^{d} u_{ij} x_i x_j。 |
| 37 | + $$ |
| 38 | + |
| 39 | +- **模型有 $O(d^2)$ 个参数**。 |
| 40 | + |
| 41 | + |
| 42 | + |
| 43 | +**线性模型 + 二阶交叉特征**: |
| 44 | +$$ |
| 45 | +p = b + \sum_{i=1}^{d} w_i x_i + \sum_{i=1}^{d} \sum_{j=i+1}^{d} u_{ij} x_i x_j。 |
| 46 | +$$ |
| 47 | + |
| 48 | +$$ |
| 49 | +u_{ij} \approx v^T_iv_j |
| 50 | +$$ |
| 51 | + |
| 52 | +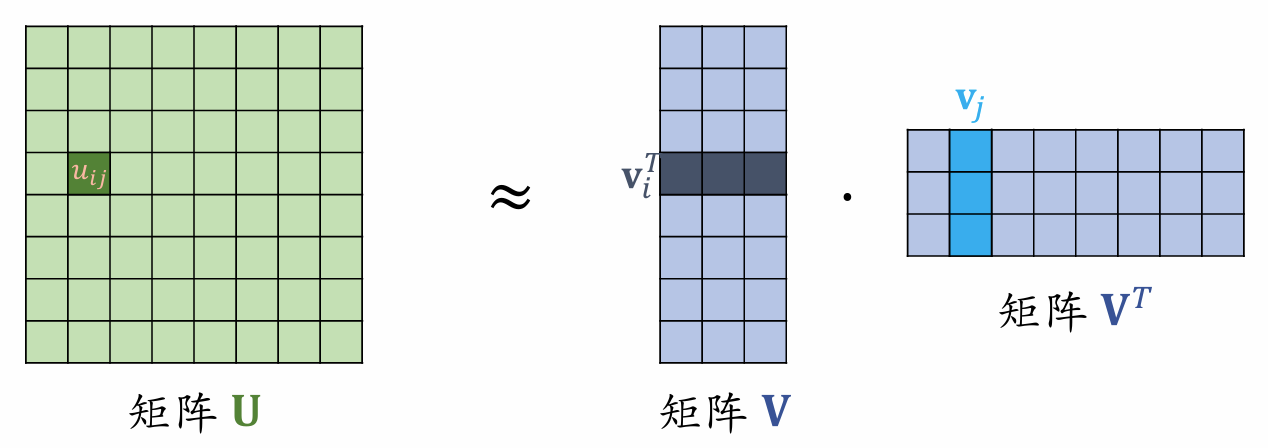 |
| 53 | + |
| 54 | +矩阵 $U$ $d$ 行 $d$ 列,矩阵 $V$ $d$ 行 $k$ 列,矩阵 $V^T$ $k$ 行 $d$ 列。 |
| 55 | + |
| 56 | +- **Factorized Machine (FM)**: |
| 57 | + |
| 58 | + $$ |
| 59 | + p = b + \sum_{i=1}^{d} w_i x_i + \sum_{i=1}^{d} \sum_{j=i+1}^{d} \left( \mathbf{v}_i^T \mathbf{v}_j \right) x_i x_j。 |
| 60 | + $$ |
| 61 | + |
| 62 | +- **FM 模型有 $O(kd)$ 个参数**。($k \ll d$) |
| 63 | + |
| 64 | +#### Factorized Machine |
| 65 | + |
| 66 | +- FM 是线性模型的替代品,能用线性回归、逻辑回归的场景,都可以用 FM。 |
| 67 | +- FM 使用二阶交叉特征,表达能力比线性模型更强。 |
| 68 | +- 通过做近似 $ u_{ij} \approx \mathbf{v}_i^T \mathbf{v}_j $,FM 把二阶交叉权重的数量从 $ O(d^2) $ 降低到 $ O(kd) $**。** |
| 69 | + |
| 70 | + |
| 71 | + |
| 72 | +### 深度交叉网络(DCN) |
| 73 | + |
| 74 | +#### 召回、排序模型 |
| 75 | + |
| 76 | +双塔模型和多目标排序模型只是结构,内部的神经网络可以用任意网络。 |
| 77 | + |
| 78 | +#### 交叉层(Cross Layer) |
| 79 | + |
| 80 | +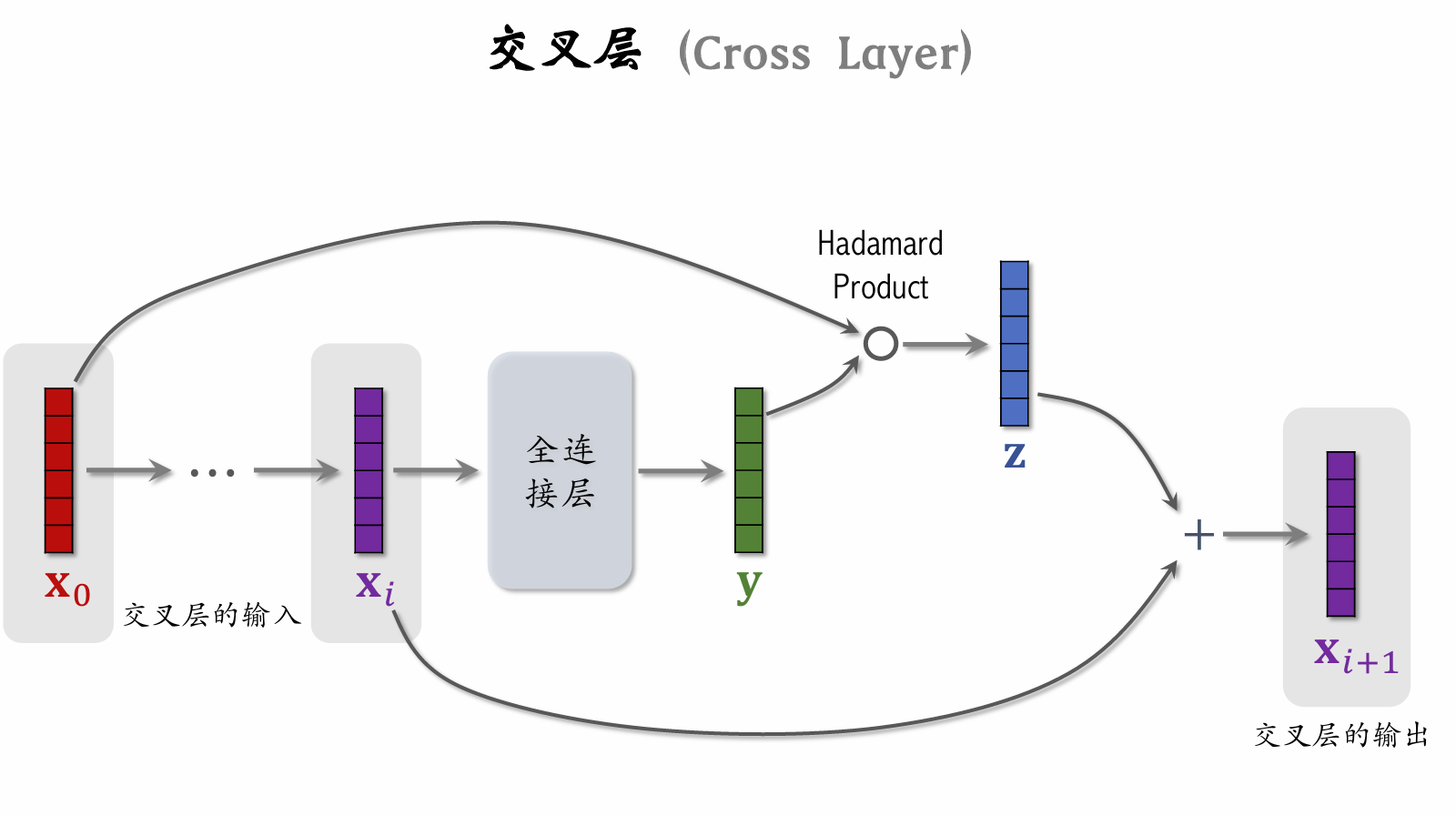 |
| 81 | + |
| 82 | +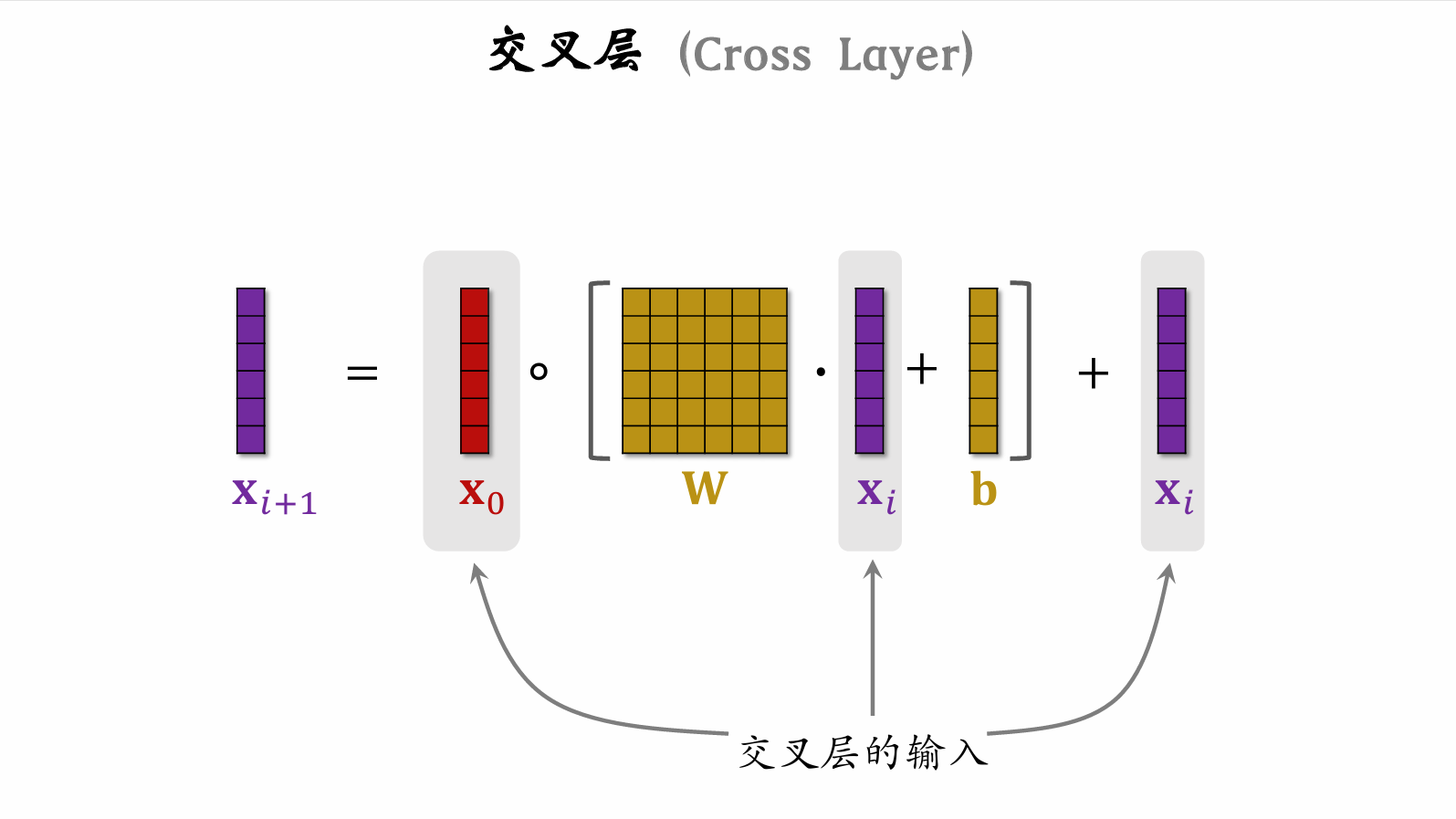 |
| 83 | + |
| 84 | +利用 Resnet 思想,防止梯度消失 |
| 85 | + |
| 86 | +#### 交叉网络 (Cross Network) |
| 87 | + |
| 88 | +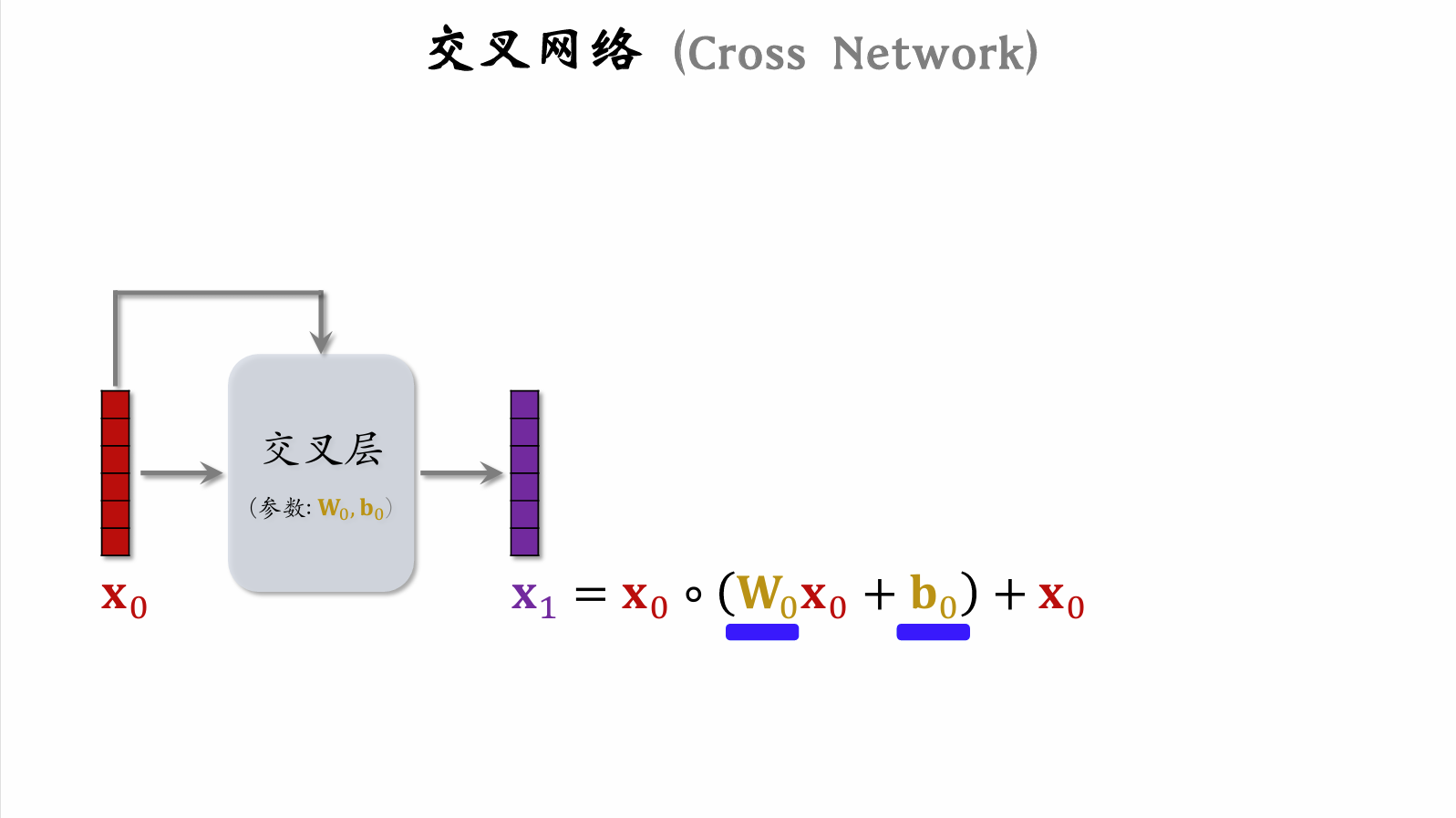 |
| 89 | + |
| 90 | +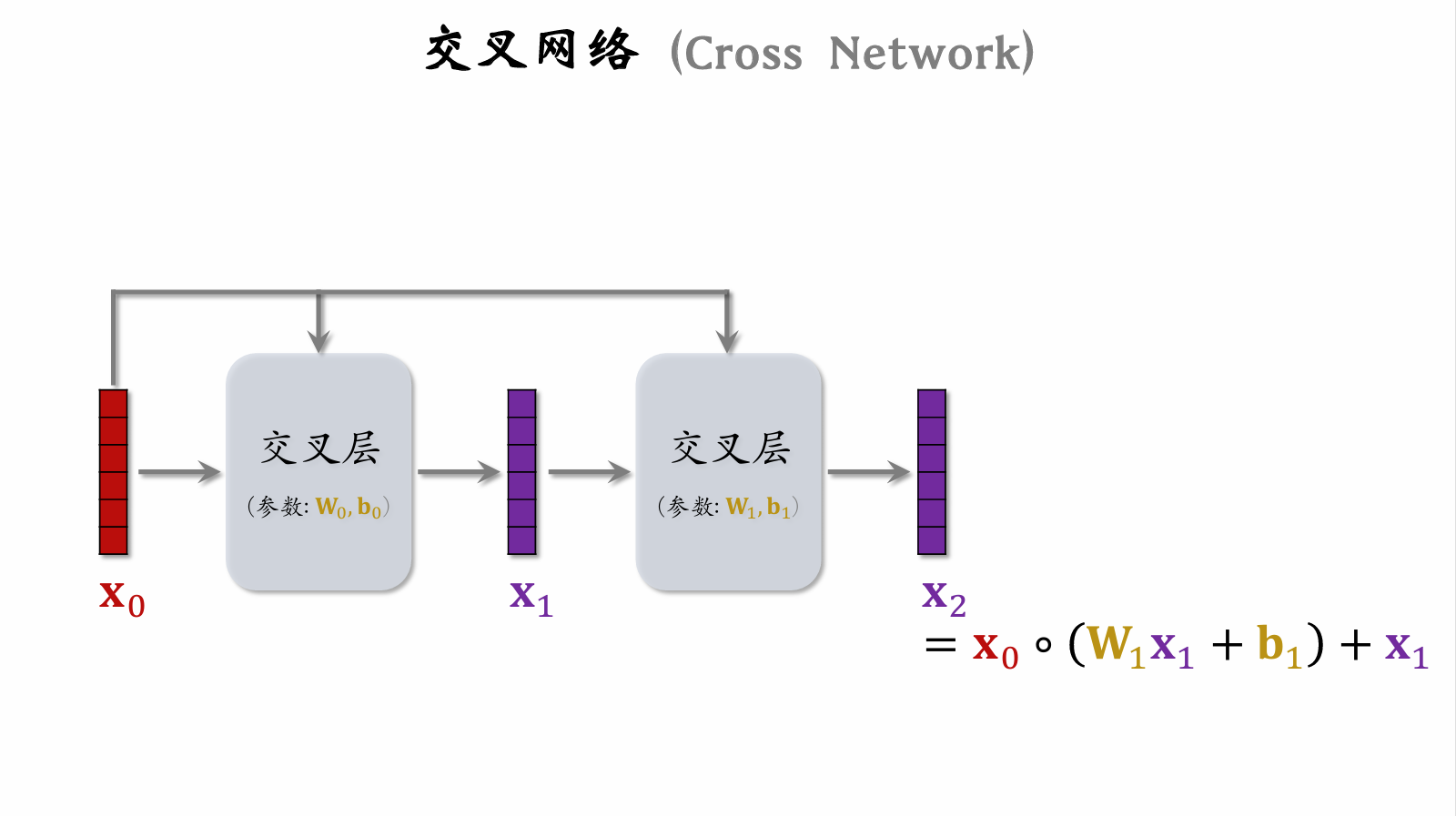 |
| 91 | + |
| 92 | +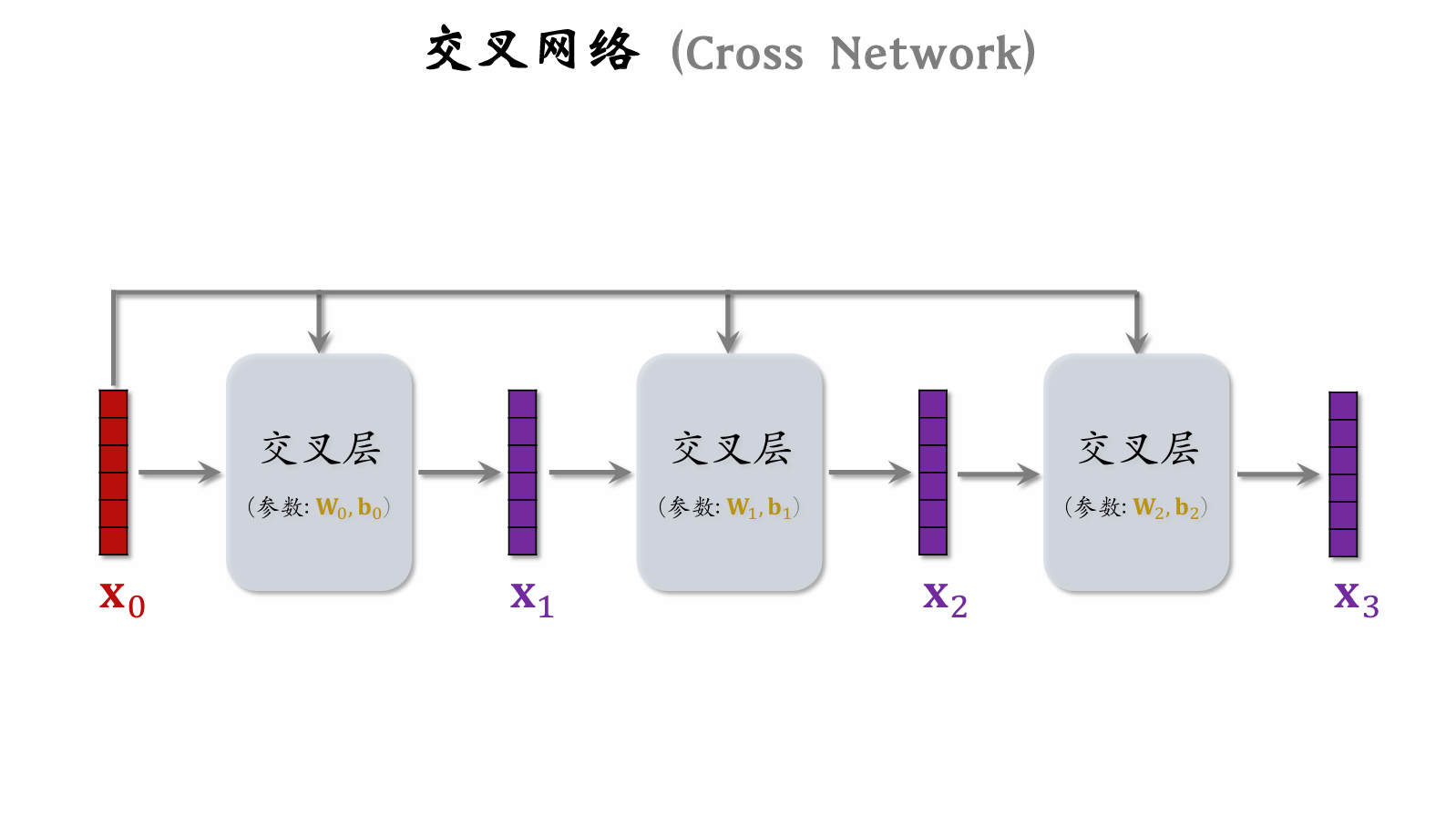 |
| 93 | + |
| 94 | +**深度交叉网络 (Deep & Cross Network)** |
| 95 | + |
| 96 | +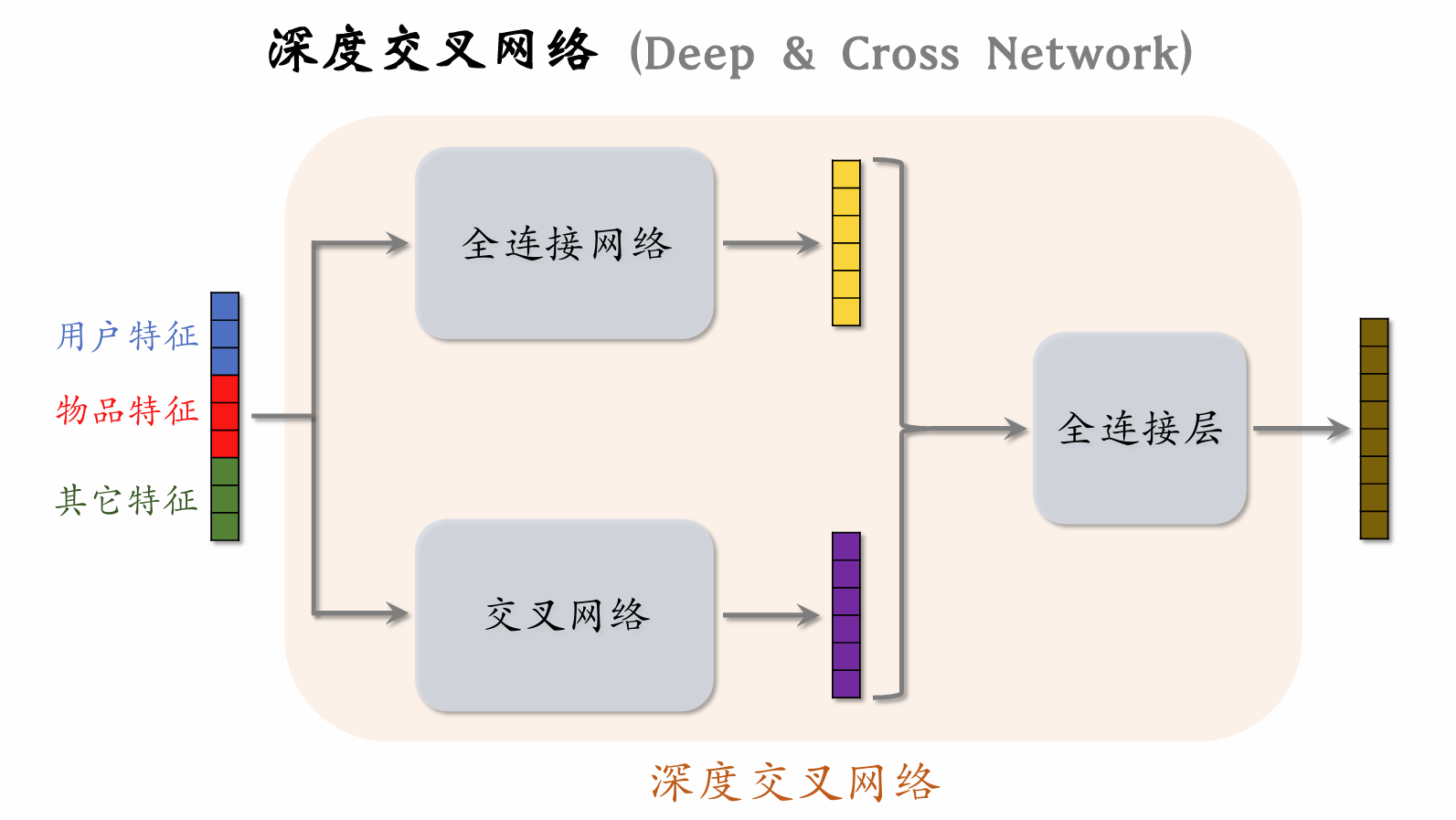 |
| 97 | + |
| 98 | +DCN 的实际效果优于全连接,可以用于双塔模型中的用户塔和物品塔,多目标排序模型中的 shared bottom 神经网络,以及MMoE中的专家神经网络。 |
| 99 | + |
| 100 | +### Learning Hidden Unit Contributions (LHUC) |
| 101 | + |
| 102 | +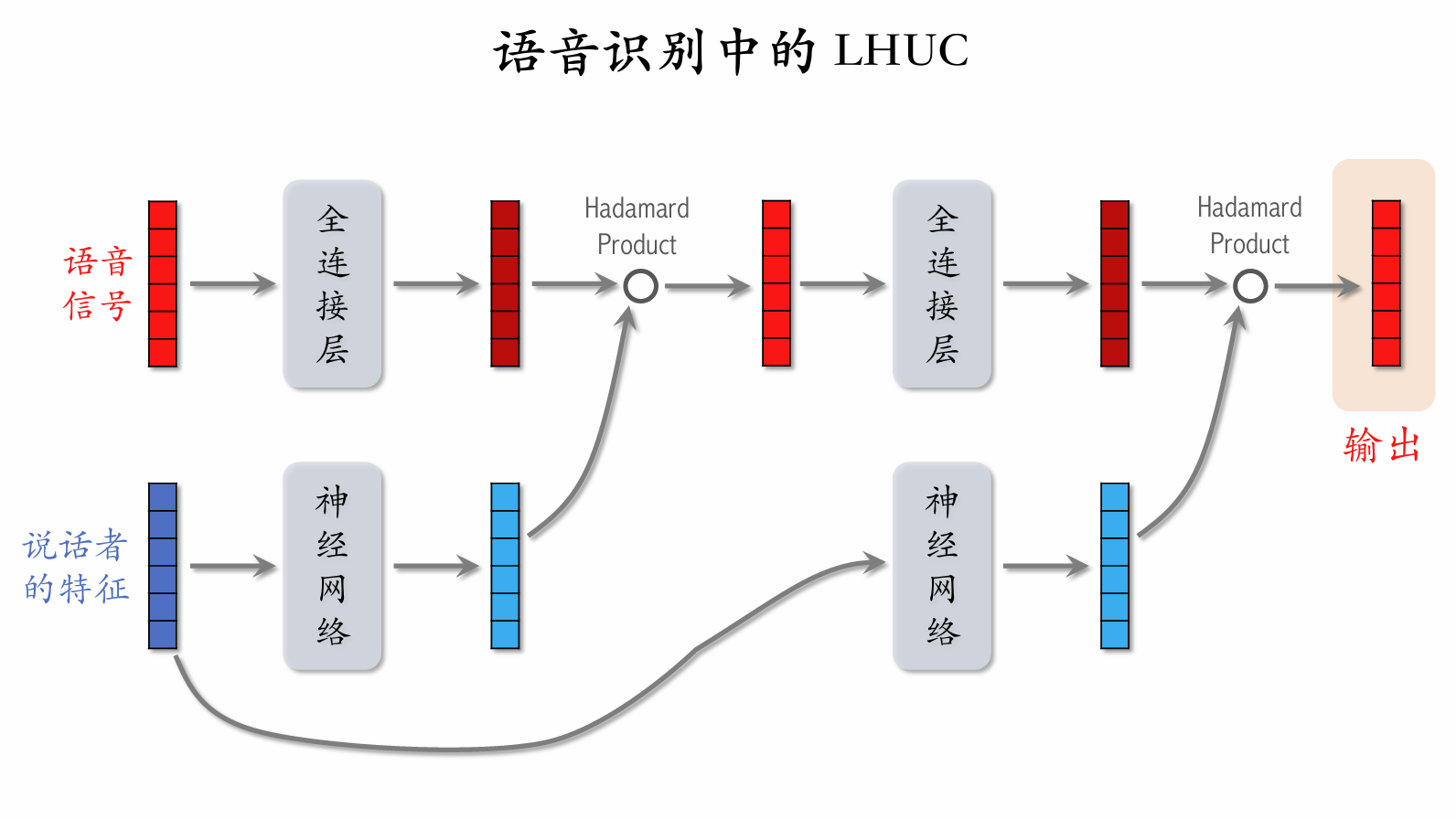 |
| 103 | + |
| 104 | +神经网络中的结构为[多个全连接层] ➝ [Sigmoid 乘以 2],这样神经网络的输出向量中都是 0 到 2 之间的数。 |
| 105 | + |
| 106 | +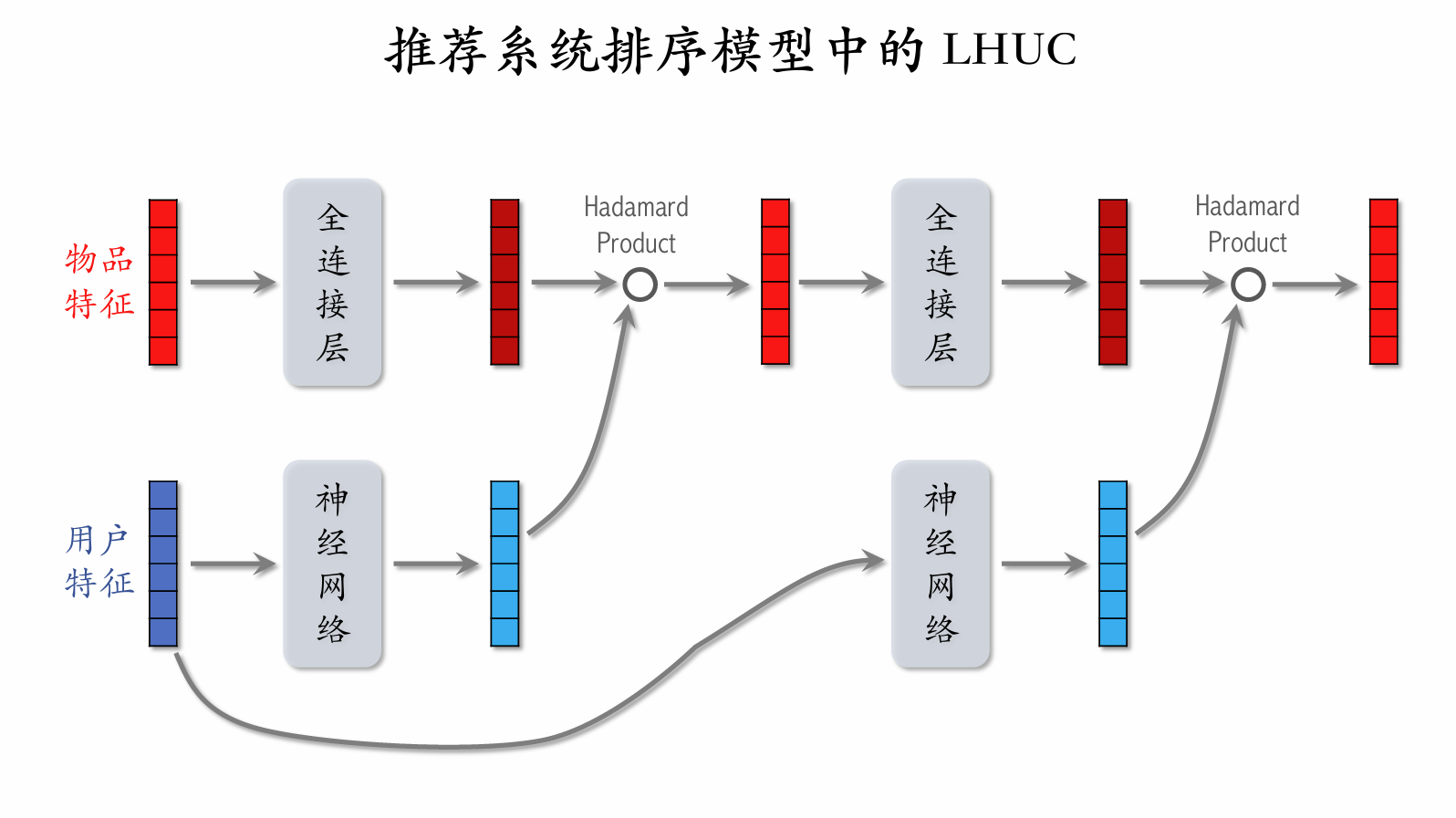 |
| 107 | + |
| 108 | + |
| 109 | + |
| 110 | +### SENet & Bilinear Cross |
| 111 | + |
| 112 | + |
| 113 | + |
| 114 | +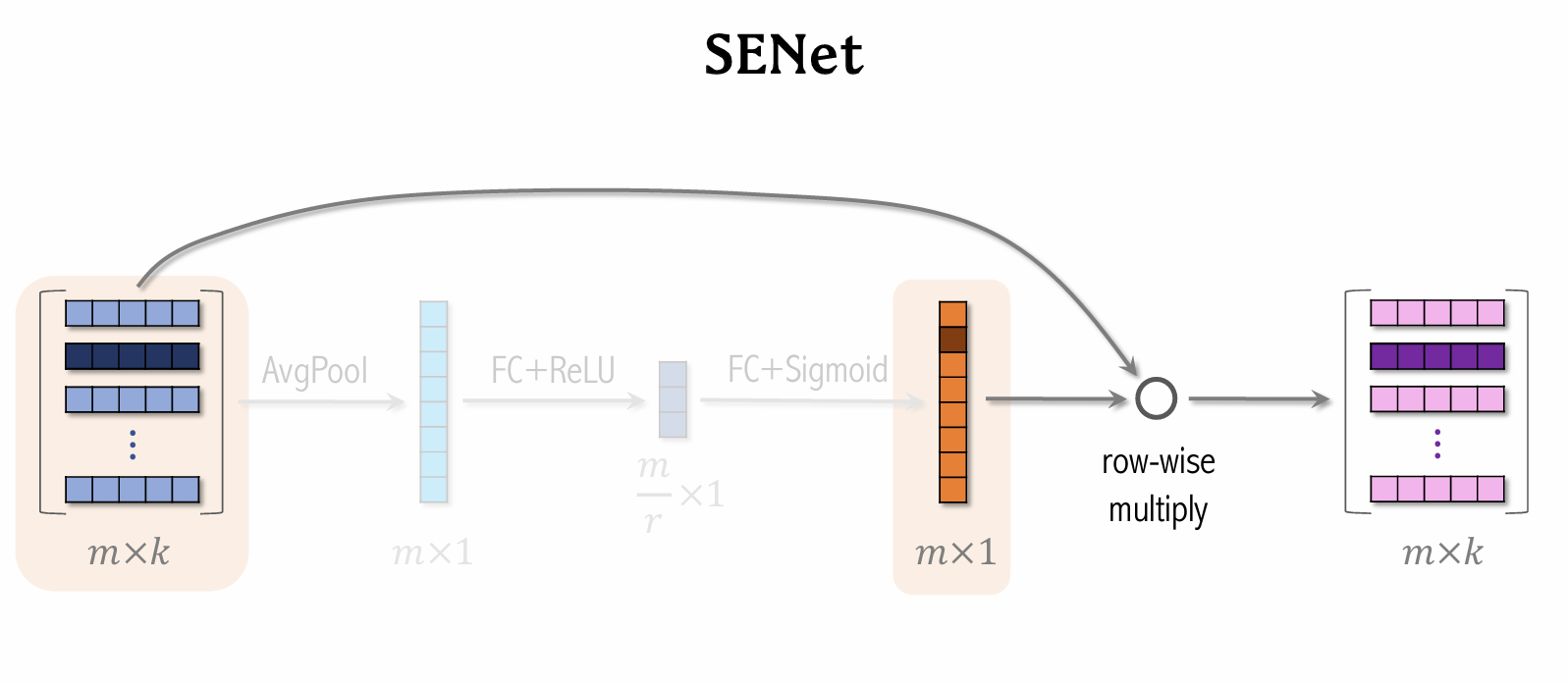 |
| 115 | + |
| 116 | +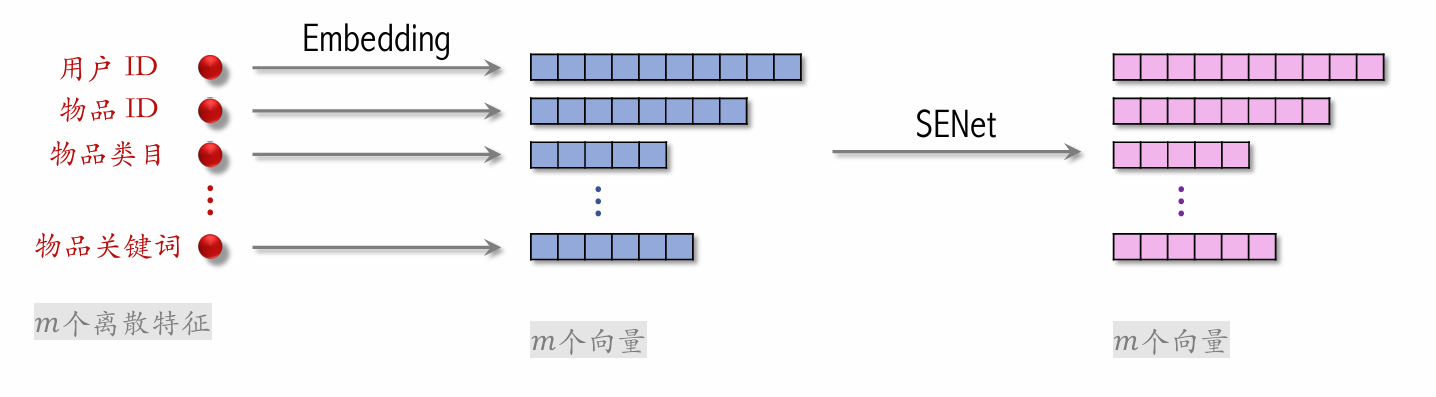 |
| 117 | + |
| 118 | +- **SENet 对离散特征做 field-wise 加权。** |
| 119 | + |
| 120 | +- **Field**: |
| 121 | + - 用户 ID Embedding 是 64 维向量。 |
| 122 | + - 64 个元素(即一个特征的 embedding 向量)算一个 field,获得相同的权重。 |
| 123 | + - 特征越重要,获得的权重越大。 |
| 124 | + |
| 125 | +- **如果有 $m$ 个 fields,那么权重向量是 $m$ 维。** |
| 126 | + |
| 127 | +#### Field 间特征交叉 |
| 128 | + |
| 129 | +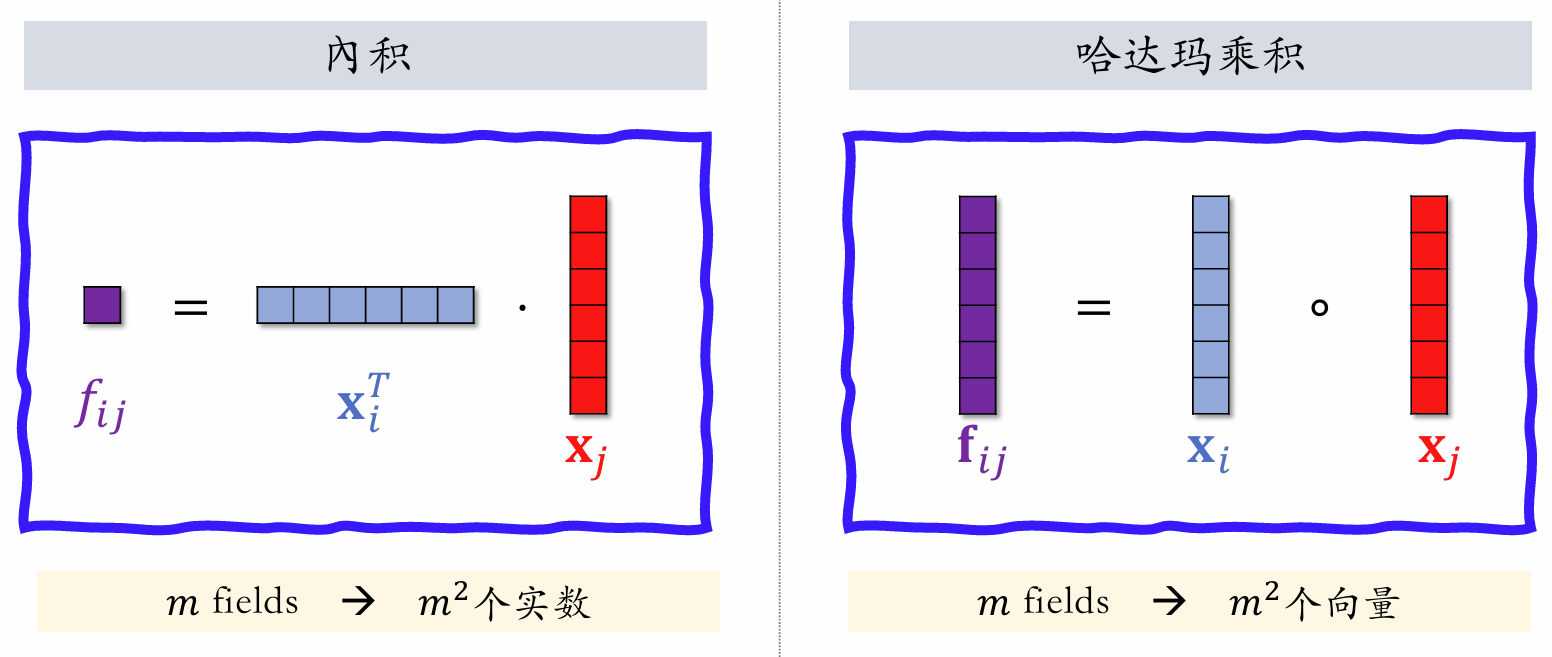 |
| 130 | + |
| 131 | +**内积** |
| 132 | + |
| 133 | +$x^T_i$ 和 $x_j$ 都是特征的 embedding 向量,$f_{ij}$ 是一个实数,如果有 $m$ 个 field,他们之间两两内积,就会有 $m^2$ 个实数。 |
| 134 | + |
| 135 | +**哈达玛乘积** |
| 136 | + |
| 137 | +$x^T_i$ 和 $x_j$ 都是特征的 embedding 向量,$f_{ij}$ 是一个向量,如果有 $m$ 个 field,他们之间两两哈达玛乘积,就会有 $m^2$ 个向量。量太大,需要人工指定一部分向量做交叉,而不是所有向量都交叉。 |
| 138 | + |
| 139 | +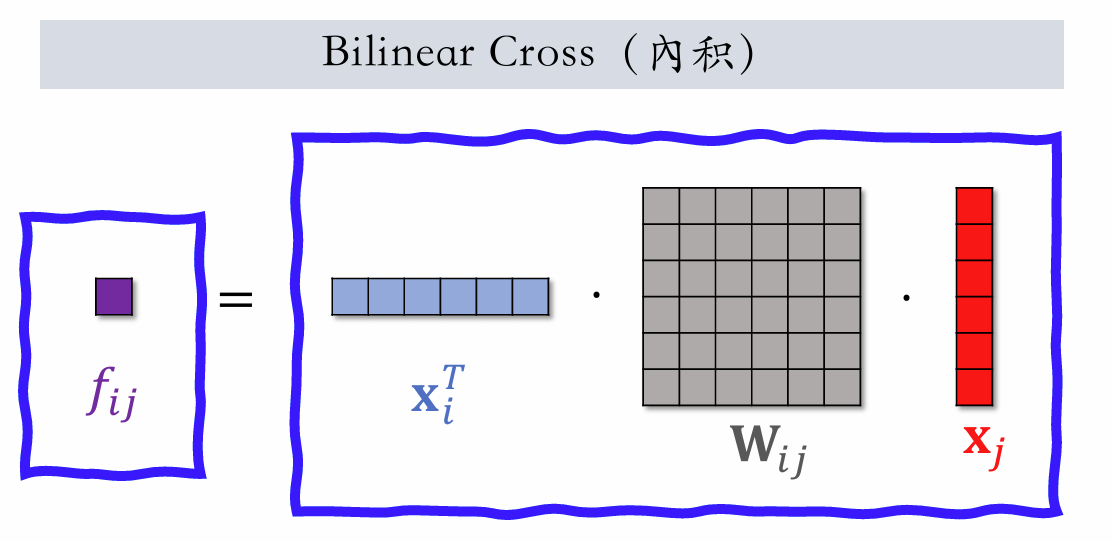 |
| 140 | + |
| 141 | +**Bilineard Cross(内积)** |
| 142 | + |
| 143 | +如果有 $m$ 个 field,就会有 $m^2$ 个实数 $f_{ij}$,$m^2/2$ 个参数矩阵 $W_{ij}$。 |
| 144 | + |
| 145 | +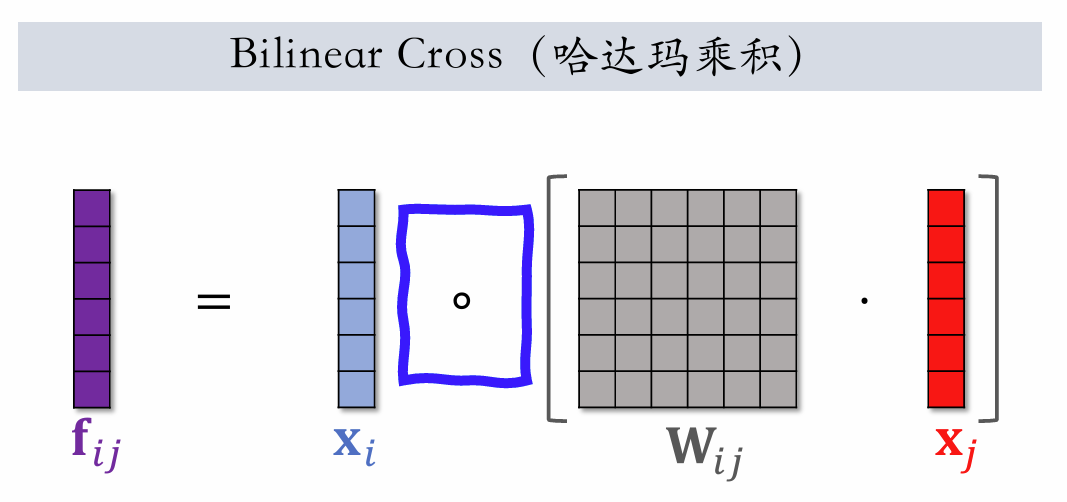 |
| 146 | + |
| 147 | +**Bilineard Cross(哈达玛)** |
| 148 | + |
| 149 | +如果有 $m$ 个 field,就会有 $m^2$ 个向量 $f_ij$,$m^2/2$ 个参数矩阵 $W_{ij}$。 |
| 150 | + |
| 151 | +#### FiBiNet |
| 152 | + |
| 153 | +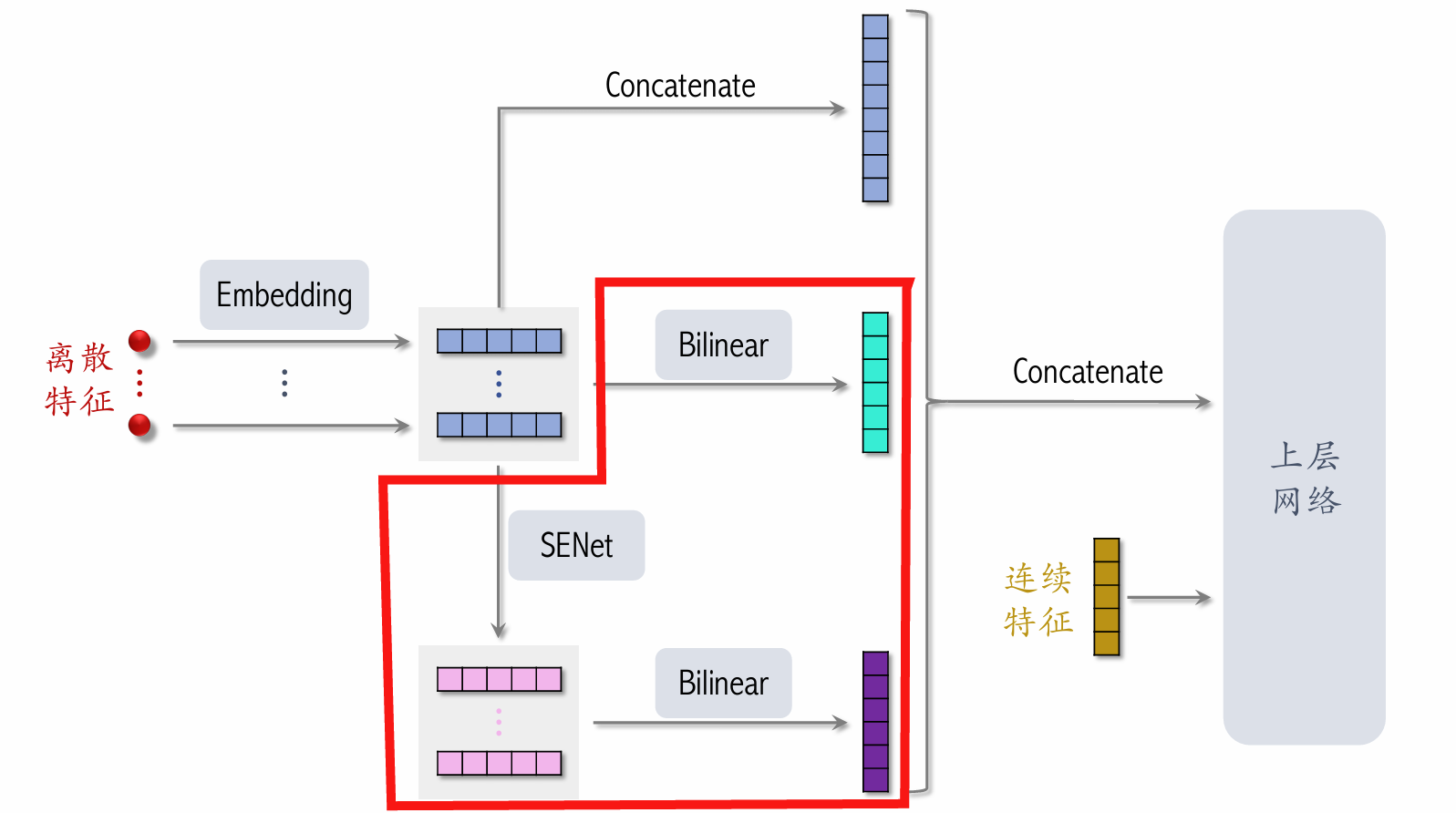 |
| 154 | + |
| 155 | + |
| 156 | + |
| 157 | +## 行为序列 |
| 158 | + |
| 159 | +### 用户行为序列建模 |
| 160 | + |
| 161 | +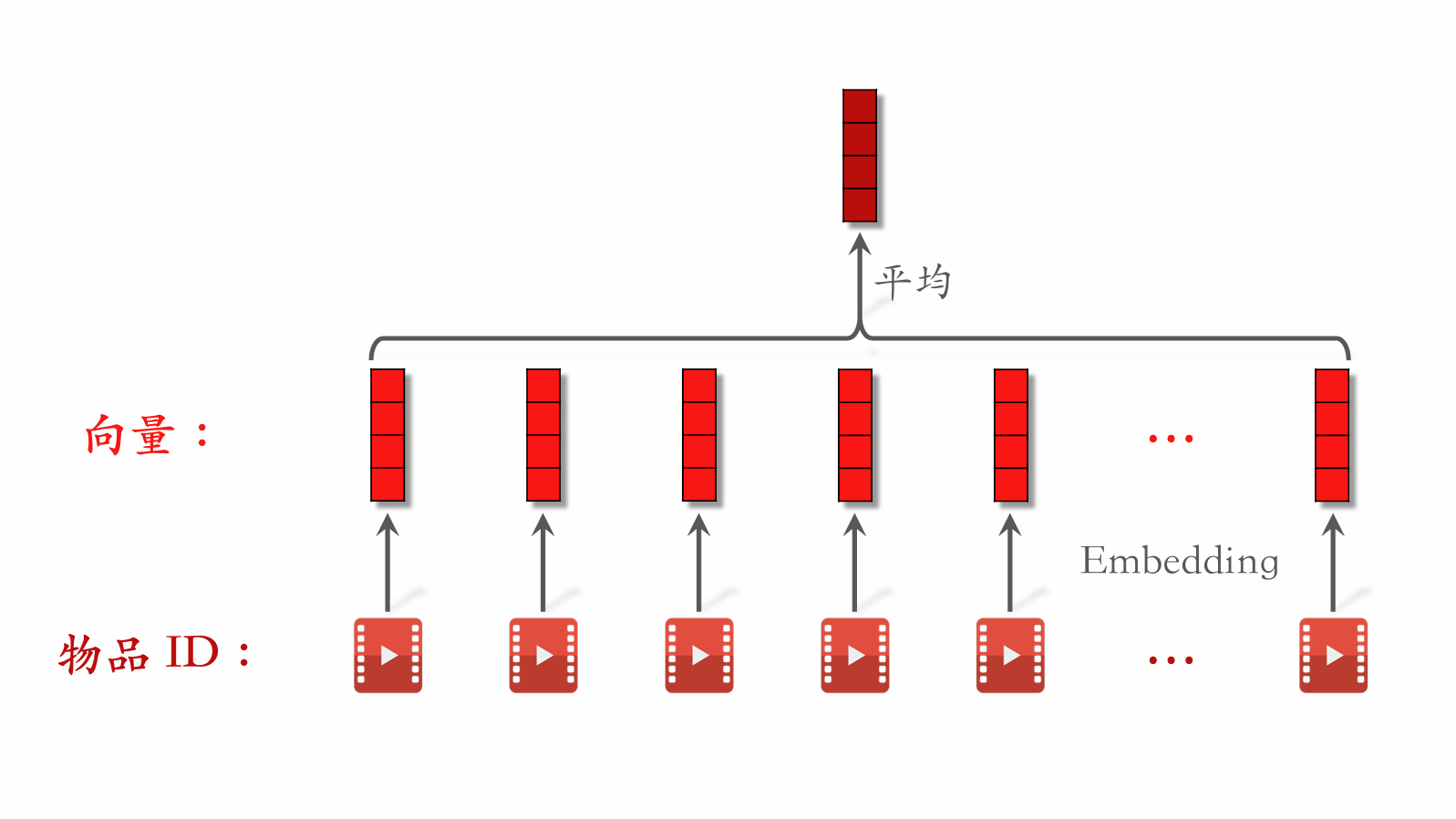 |
| 162 | + |
| 163 | + **LastN 特征** |
| 164 | + |
| 165 | +- **LastN**:用户最近的 $n$ 次交互(点击、点赞等)的物品 ID。 |
| 166 | +- 对 **LastN** 物品 ID 做 embedding,得到 $n$ 个向量。 |
| 167 | +- 把 $n$ 个向量取平均,作为用户的一种特征。 |
| 168 | +- 适用于召回双塔模型、粗排三塔模型、精排模型。 |
| 169 | + |
| 170 | +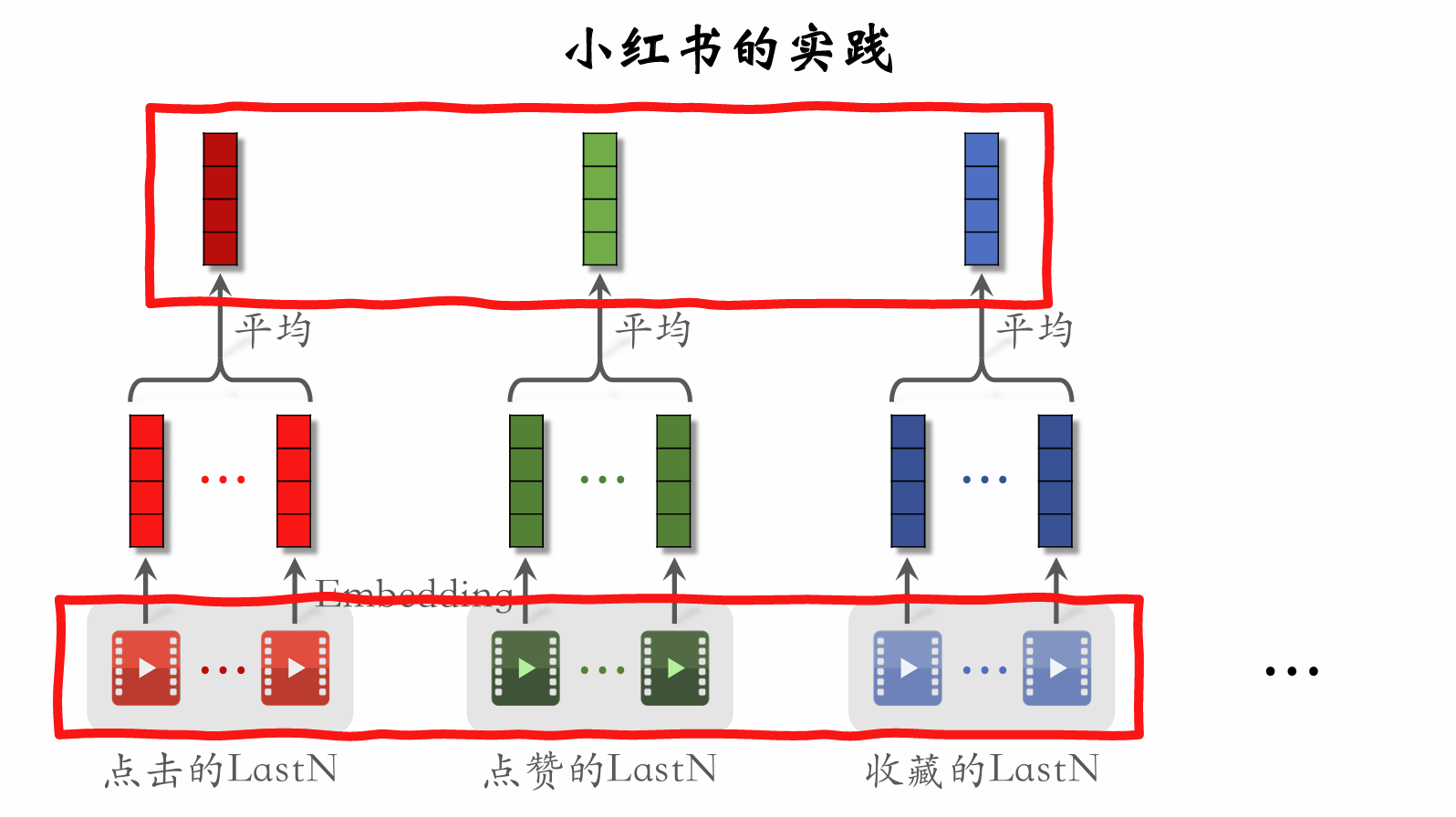 |
| 171 | + |
| 172 | +### DIN 模型 |
| 173 | + |
| 174 | +**DIN 模型** |
| 175 | + |
| 176 | +- DIN 用 加权平均 代替 平均,即注意力机制(attention)。 |
| 177 | +- 权重:候选物品与用户 **LastN** 物品的相似度。 |
| 178 | + |
| 179 | +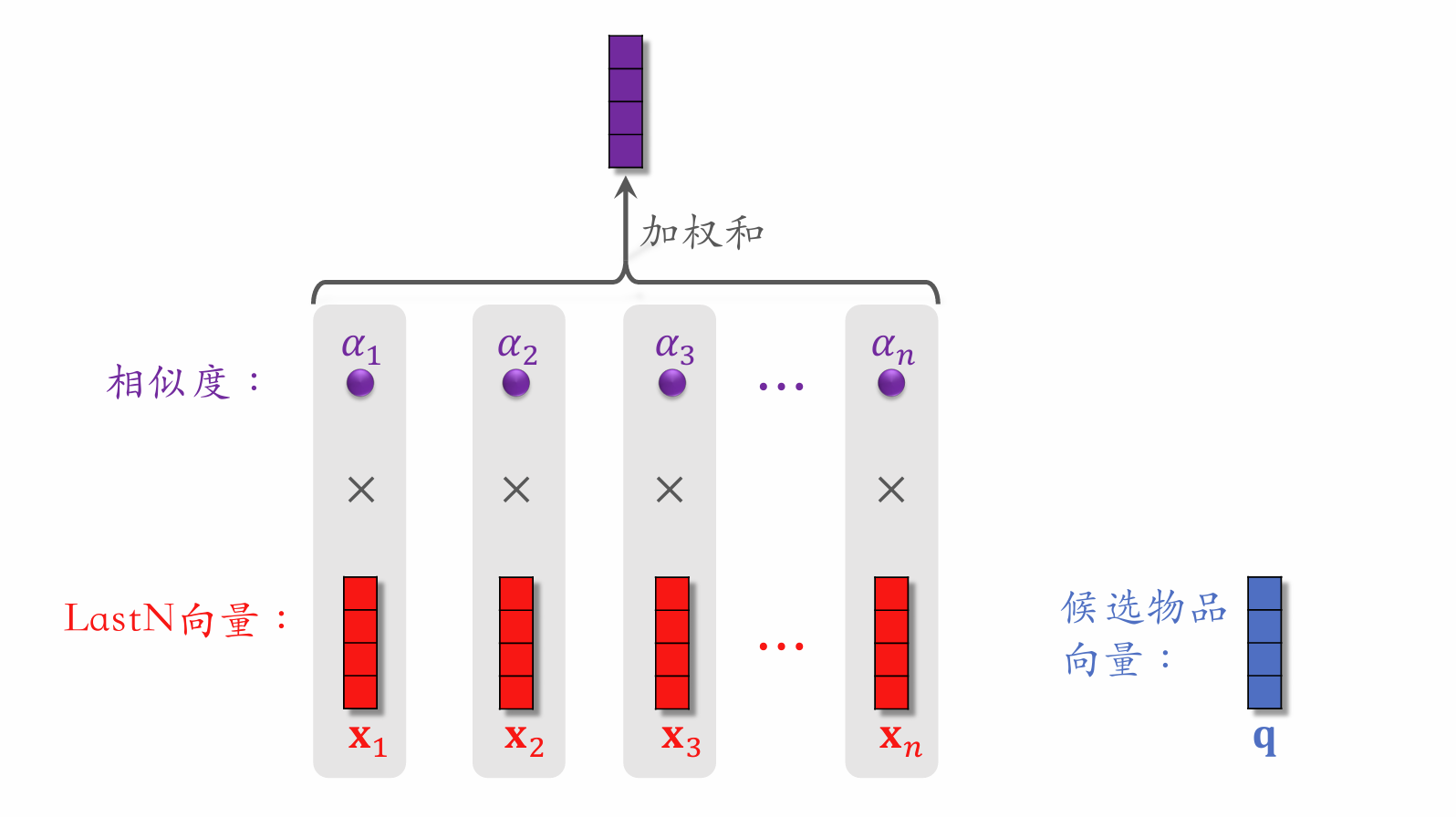 |
| 180 | + |
| 181 | +**DIN 模型** |
| 182 | + |
| 183 | +- 对于某候选物品,计算它与用户 **LastN** 物品的相似度。 |
| 184 | +- 以相似度为权重,求用户 **LastN** 物品向量的加权和,结果是一个向量。 |
| 185 | +- 把得到的向量作为一种用户特征,输入排序模型,预估(用户,候选物品)的点击率、点赞率等指标。 |
| 186 | +- 本质是注意力机制(attention)。 |
| 187 | + |
| 188 | +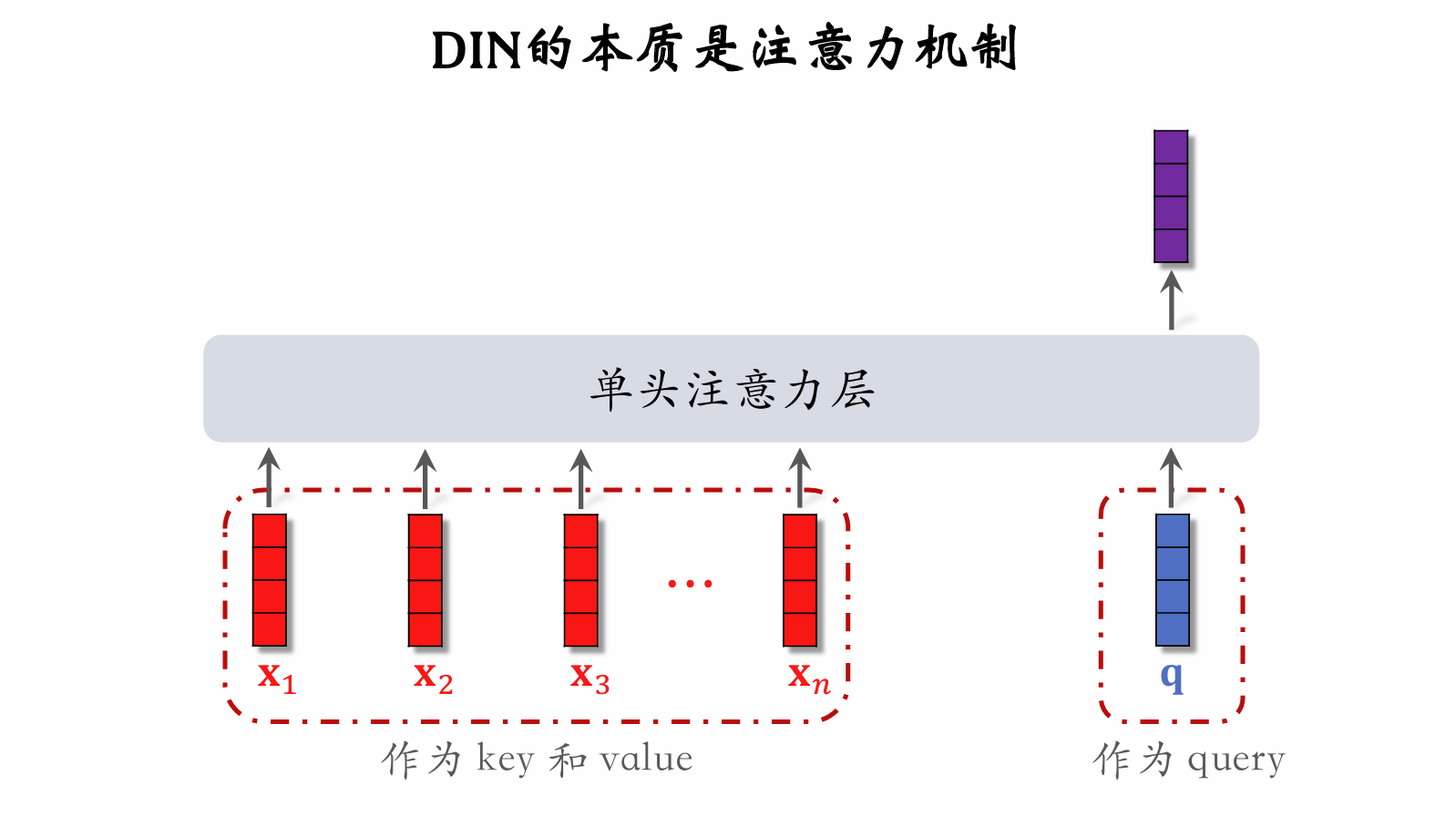 |
| 189 | + |
| 190 | +**简单平均 v.s 注意力机制** |
| 191 | + |
| 192 | +- *简单平均* 和 注意力机制 都适用于精排模型。 |
| 193 | +- *简单平均* 适用于双塔模型、三塔模型。 |
| 194 | + - *简单平均* 只需要用到 **LastN**,属于用户自身的特征。 |
| 195 | + - 把 LastN 向量的平均作为用户塔的输入。 |
| 196 | +- 注意力机制 不适用于双塔模型、三塔模型。 |
| 197 | + - 注意力机制 需要用到 **LastN** + **候选物品**。 |
| 198 | + - 用户塔看不到候选物品,不能把 注意力机制 用在用户塔。 |
| 199 | + |
| 200 | +### SIM模型 |
| 201 | + |
| 202 | +**DIN 模型** |
| 203 | + |
| 204 | +- 计算用户 **LastN** 向量的加权平均。 |
| 205 | +- 权重是候选物品与 LastN 物品的相似度。 |
| 206 | + |
| 207 | +**DIN 模型的缺点** |
| 208 | + |
| 209 | +- 注意力层的计算量 $\propto n$(用户行为序列的长度)。 |
| 210 | +- 只能记录最近几百个物品,否则计算量太大。 |
| 211 | +- 缺点:关注短期兴趣,遗忘长期兴趣。 |
| 212 | + |
| 213 | +**如何改进** **DIN**? |
| 214 | + |
| 215 | +- **目标**:保留用户长期行为序列($n$ 很大),而且计算量不会过大。 |
| 216 | + |
| 217 | +- **改进 DIN**: |
| 218 | + - DIN 对 **LastN** 向量做加权平均,权重是相似度。 |
| 219 | + - 如果某 **LastN** 物品与候选物品差异很大,则权重接近零。 |
| 220 | + - 快速排除掉与候选物品无关的 **LastN** 物品,降低注意力层的计算量。 |
| 221 | + |
| 222 | +#### SIM 模型 |
| 223 | + |
| 224 | +- 保留用户长期行为记录,$n$ 的大小可以是几千。 |
| 225 | +- 对于每个候选物品,在用户 **LastN** 记录中做快速查找,找到 $k$ 个相似物品。 |
| 226 | +- 把 **LastN** 变成 **TopK**,然后输入到注意力层。 |
| 227 | +- **SIM** 模型减小计算量(从 $n$ 降到 $k$)。 |
| 228 | + |
| 229 | +**第一步:查找** |
| 230 | + |
| 231 | +- **方法一:Hard Search** |
| 232 | + - 根据候选物品的类别,保留 **LastN** 物品中类别相同的。 |
| 233 | + - 简单,快速,无需训练。 |
| 234 | + |
| 235 | +- **方法二:Soft Search** |
| 236 | + - 把物品做 **embedding**,变成向量。 |
| 237 | + - 把候选物品向量作为 **query**,做 $k$ 近邻查找,保留 **LastN** 物品中最近的 $k$ 个。 |
| 238 | + - 效果更好,编程实现更复杂。 |
| 239 | + |
| 240 | + |
| 241 | + |
| 242 | +**第二步:注意力机制** |
| 243 | + |
| 244 | +**使用时间信息** |
| 245 | + |
| 246 | +- 用户与某个 **LastN** 物品的交互时刻距离今为 $\delta$。 |
| 247 | +- 对 $\delta$ 做离散化,再做 **embedding**,变成向量 **d**。 |
| 248 | +- 把两个向量做 **concatenation**,表征一个 **LastN** 物品。 |
| 249 | + - 向量 **x** 是物品 **embedding**。 |
| 250 | + - 向量 **d** 是时间的 **embedding**。 |
| 251 | + |
| 252 | +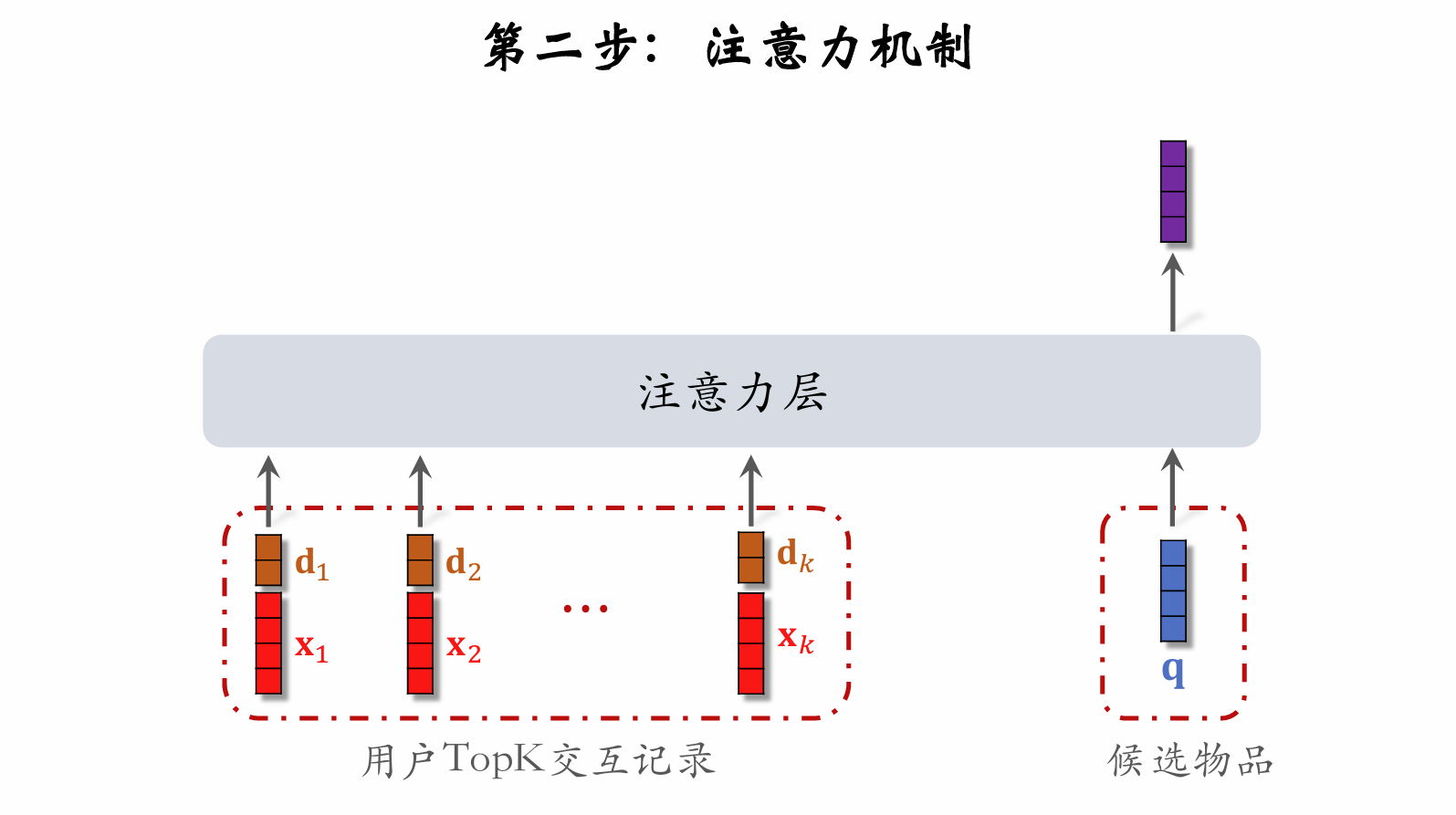 |
| 253 | + |
| 254 | +为什么 SIM **使用时间信息**? |
| 255 | + |
| 256 | +- **DIN** 的序列短,记录用户近期行为。 |
| 257 | +- **SIM** 的序列长,记录用户长期行为。 |
| 258 | +- 时间越久远,重要性越低。 |
| 259 | + |
| 260 | +#### 结论 |
| 261 | + |
| 262 | +- 长序列(长期兴趣)优于短序列(近期兴趣)。 |
| 263 | +- 注意力机制 优于 简单平均。 |
| 264 | +- **Soft search** 还是 **Hard search**?取决于工程基建。 |
| 265 | +- 使用时间信息有提升。 |
| 266 | + |
| 267 | + |
0 commit comments