Merge branch 'master' into ctm/doc/tests-in-github-actions

Author: carlosmartinezthrasio

docs/machine_learning/introduction.md docs/machine_learning/1_introduction.mddocs/machine_learning/introduction.md renamed to docs/machine_learning/1_introduction.md

@@ -0,0 +1,108 @@
+# Regression
+
+Regression, along with classification, are the most common machine learning techniques.
+The difference between them is that in regression the algorithms are used to predict
+continuous outcome. Regression machine learning models live in the group of
+supervised learning where the output variable (dependent variable) is known, and
+numeric. The goal is to understand and model the relationship between the
+dependent variable (what we want to predict), and one or more independent variables.
+
+```mermaid
+flowchart BT
+    A[Supervised Learning]---E[Machine Learning]
+    B[Unsupervised Learning]---E[Machine Learning]
+    C[Semi-Supervised Learning]---E[Machine Learning]
+    D[Reinforcement Learning]---E[Machine Learning]
+    F[Classification]---A[Supervised Learning]
+    G[Regression]---A[Supervised Learning]
+    H[Clustering]---B[Unsupervised Learning]
+    style G stroke:#f66,stroke-width:4px
+```
+
+## Linear Regression
+
+- Statistical method used to model the relationship between a dependent variable and
+  one or more independent variables.
+
+- Assumes that the relationship between the dependent variable and the
+  independent variable(s) is linear.
+
+<strong>Training</strong>: find the line of best fit that minimizes the sum of
+squared differences between the predicted values and the actual values of the
+dependent variable.
+
+The equation of the hyperplane (n independent variables) is given by:
+
+y = b0 + b1X1 + b2X2 + ... + bn\*Xn
+
+In the simplest form (only one independent variable), the equation is the same
+as the straight line equation.
+
+y = b0 + b1X1
+
+<figure markdown>
+  ![Linear Regression Model](./assets/linear-regression.png){ width="400" }
+    <figcaption>
+        Linear Regression Model. Adapted from "Linear Regression in Machine Learning”. 
+        Retrieved from [here](https://www.javatpoint.com/linear-regression-in-machine-learning).
+    </figcaption>
+</figure>
+
+Before using linear regression model, make sure that the data follow these assumptions:
+
+1. The variables should be measured at a continuous level.
+
+2. Relationship between the dependent variable and the independent variable(s) is linear
+   (scatter plot to visualize).
+
+3. The observations and variables should be independent of each other.
+
+4. Your data should have no significant outliers.
+
+5. The residuals (errors) of the best-fit regression line follow normal distribution.
+
+## Polynomial Regression
+
+Polynomial Regression is very similar to Linear Regression. The only difference is that
+it transforms the input data to include non-linear terms. It is described
+by a degree, which is the highest power computed from the original input. The amount
+of additional terms will consequently depend on the degree.
+
+A dataset with a single feature X
+
+```
+X = [
+    [X1],
+    [X2],
+    [X3],
+]
+```
+
+using a polynomial of second degree would be transformed to:
+
+```
+X = [
+    [X1, X1²],
+    [X2, X2²],
+    [X3, X3²],
+]
+```
+
+<figure markdown>
+  ![Polynomial Regression Model](./assets/linear-vs-poly.png){ width="500" }
+    <figcaption>
+        Linear vs Polynomial Regression. Adapted from "Why -Polynomial Regression and not Linear Regression?” by Tamil Selvi. 
+        Retrieved from [here](https://www.numpyninja.com/post/why-polynomial-regression-and-not-linear-regression).
+    </figcaption>
+</figure>
+
+The training process would be exactly the same: find the coefficients
+for each of the features that minimizes the square error. In the described example,
+since we would have 2 coefficients instead of 1, it would define a parable instead of
+a straight line.
+
+Key factors to consider:
+
+- Include nonlinear terms such as 𝑥².
+- Often used when the relationship between the variables cannot be accurately described by a linear model.
+- Plot the data (Ex: scatter plot) and check if a linear model is appropriate.

docs/machine_learning/2_regression.md

@@ -0,0 +1,203 @@
+# Model Evaluation
+
+Before deploying a model to be consumed by several applications,
+we need to know what is the expected performance that it will achieve.
+After training a model using the collected and transformed dataset,
+concrete metrics have to be calculated so we can have a vision of
+how well the algorithm can model the data that we have on hand.
+
+Depending on the type of the problem (supervised, unsupervised,
+classification, regression), there are different metrics
+to evaluate. In supervised learning, we have available target values
+that we can use to compare to what was predicted by the model.
+However, the metrics are different between classification and regression problems
+since in the first one the target variable is not continuous.
+
+Another topic worth mentioning, that can lead to misleading conclusions,
+is what data should be used to evaluate. If we train
+the model with the entire dataset, make predictions over the same dataset,
+and compare these predictions with the actual values, we are not
+verifying how the model behaves with unseen data samples. That's why
+before speaking about evaluation metrics, we have to jump into
+data split strategies, to be able to separate the data into
+different sets depending on their use.
+
+## Data Split Strategies
+
+A data split strategy is a way of splitting the data
+into different subsets, so each subset is used with a different goal.
+This will prevent us from using the entire dataset for training, tuning
+, and evaluating which can give false conclusions.
+
+The most used strategies are:
+
+- train-test split
+- cross-validation
+- leave one out
+
+### Train-test split
+
+The idea behind the train-test split, as the name suggests, is to split
+the entire dataset in different sets, usually the following:
+
+- training set (usually ~70%): data samples used to train the model
+- validation set (usually ~15%): data samples used to tune the model
+  (hyperparameters, architecture)
+- testing set (usually ~15%): data samples used to evaluate the model
+
+<figure markdown>
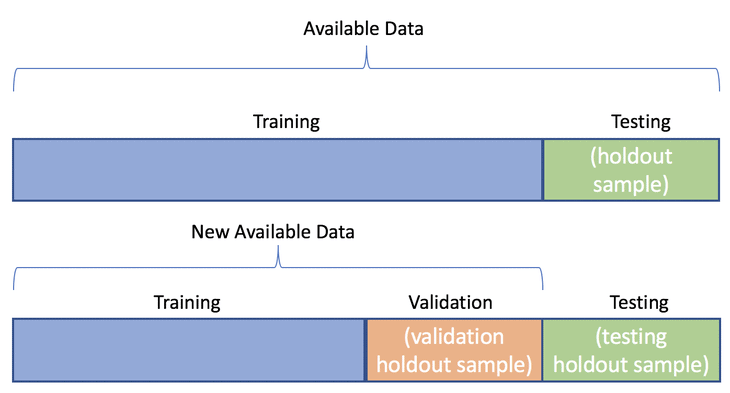+  ![Train-test Split](https://cdn.shortpixel.ai/spai/q_lossy+w_730+to_webp+ret_img/https://algotrading101.com/learn/wp-content/uploads/2020/06/training-validation-test-data-set.png){ width="500" }
+    <figcaption>
+        Train-Test Split. Adapted from "Train/Test Split and Cross Validation – A Python Tutorial” by Greg Bland. 
+        Retrieved from [here](https://algotrading101.com/learn/train-test-split/).
+    </figcaption>
+</figure>
+
+### Cross-validation
+
+Cross-validation, and leave one out are strategies used usually when
+the dataset size is not huge, since they are computationally expensive.
+The idea is to divide the entire dataset into K folds. The model
+will be trained using N - 1 folds and evaluated on the remaining fold.
+These will be performed K (number of folds) times, so the advantage is that
+the data coverage will be higher (more reliable evaluation).
+
+<figure markdown>
+  ![Cross-validation](https://scikit-learn.org/stable/_images/grid_search_cross_validation.png){ width="500" }
+    <figcaption>
+        Cross Validation. Adapted from "Cross-validation: evaluating estimator performance”. 
+        Retrieved from [here](https://scikit-learn.org/stable/modules/cross_validation.html).
+    </figcaption>
+</figure>
+
+### Leave one out
+
+Leave one out is usually applied on small datasets. It is a particular case
+of cross-validation, it is equivalent to using cross-validation with
+N folds, given that N is the number of samples in the dataset.
+This means that the model will be trained and evaluated N times,
+and the prediction for evaluation will be performed on a single
+sample at a time.
+
+### To be aware
+
+It is worth mentioning two additional topics:
+
+- temporal data: when dealing with temporal data, it is
+  important to sort before applying the split, because
+  it is considered "cheating" if the sort operation
+  is not applied. Imagine having past and future samples
+  in the training set of a sample in the test set. This
+  would not reflect the real usage of the model;
+
+- stratification: in classification problems, it is important
+  to maintain the class distribution along the different sets,
+  so we can avoid having, for example, a test set with samples
+  of a single class.
+
+## Evaluation Metrics
+
+Evaluation metrics can be divided into regression and classification
+since the output is different depending on the type of the problem.
+However, the goal of these metrics is to evaluate how well the model
+can make predictions. It receives as input the actuals (y) and
+the predicted values for the same samples (ŷ).
+
+### Regression
+
+In regression, the actuals and the predicted values are continuous.
+The following metrics are usually used to evaluate this kind of models:
+
+- Mean Absolute Error (MAE)
+
+MAE is the easiest metric to interpret. It represents how much
+the predicted value deviates from the actual value. n is the number
+of samples (size of y and ŷ).
+
+`MAE = (1/n) * Σ|yi - ŷi|`
+
+- Mean Square Error (MSE)
+
+MSE is very similar to MAE. The difference is that it is squared instead
+of using the absolute difference. This will penalize
+higher errors. It is usually used as a loss function in some of the
+models (i.e Neural Network).
+
+`MSE = (1/n) * Σ(yi - ŷi)²`
+
+- Root Mean Square Error (RMSE)
+
+RMSE is the root of MSE. This facilitates the interpretation
+since it converts the unit from squared to the original unit.
+
+`RMSE = sqrt((1/n) * Σ(yi - ŷi)²)`
+
+- R-Squared Score (R2)
+
+R2 is a metric that represents how much variance of the data
+was successfully modeled. It indicates how well the model
+could represent the data and can establish a relationship
+between the independent variables and the dependent variable.
+
+SSres is the residual sum of squares, and SStot is the
+total variance contained in the target output y. This metric is
+within the range of 0.0 to 1.0, being 1.0 a perfect model, able to
+represent the entire variance. It can also have negative values
+in cases where there is a terrible relationship between the
+target and independent variables.
+
+`R2 = 1 - (SSres / SStot)`
+
+## Useful Plots
+
+Visualization sometimes can help taking conclusions about the
+obtained results. The listed metrics in the previous section
+are good to have a clear and specific evaluation of the model.
+However, some useful plots can be visualized to
+complement the achieved numeric results.
+
+### Regression
+
+The first plot is the actuals vs predicted values.
+Ideally, all the points should be laid in the diagonal line,
+which represents that the predicted value is equal to the
+actual value. This plot gives an overall idea of the
+achieved predictions and how far they are from the actual value.
+
+<figure markdown>
+  ![Actual vs Predicted plot](https://i.stack.imgur.com/FJi0n.png){ width="400" }
+    <figcaption>
+        Actual vs Predicted plot. 
+        Retrieved from [here](https://stats.stackexchange.com/questions/333037/interpret-regression-model-actual-vs-predicted-plot-far-off-of-y-x-line).
+    </figcaption>
+</figure>
+
+The second one is similar, however, the residual value
+substitutes one of the previous variables (actuals or predictions).
+Ideally, the points should be near 0.0 which means no error.
+The goal of this plot is to conclude the error for each
+range of values and visualize possible trends that the errors
+may show. This indicates that there is some pattern contained in
+the data that the model was not able to cover.
+
+<figure markdown>
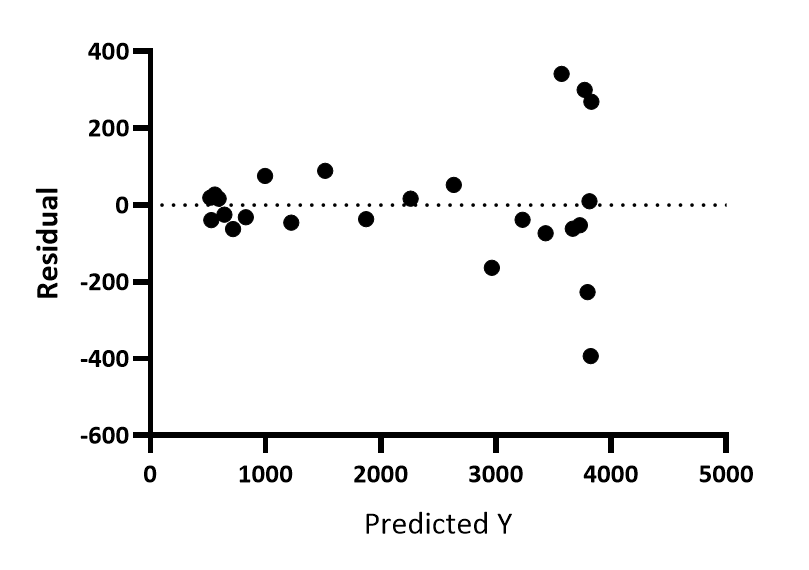+  ![Residuals vs Predicted plot](https://www.graphpad.com/guides/prism/latest/curve-fitting/images/reg_clip0154.png){ width="400" }
+    <figcaption>
+        Residuals vs Predicted plot. Adapted from "Residual plot".
+        Retrieved from [here](https://www.graphpad.com/guides/prism/latest/curve-fitting/reg_fit_tab_residuals_2.htm).
+    </figcaption>
+</figure>
+
+The last one is the histogram of residuals. This allows the
+conclusion of where are most errors contained. Additionally,
+it is also important to conclude the distribution of the errors.
+For example, a Linear Regression assumes that the errors are normally
+distributed.
+
+<figure markdown>
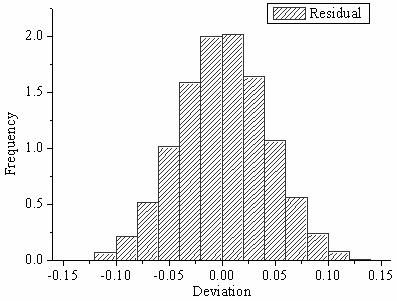+  ![Residuals Histogram](https://d2mvzyuse3lwjc.cloudfront.net/doc/en/UserGuide/images/Graphic_Residual_Analysis/Graphic_Residual_Analysis-5.jpg?v=10739){ width="400" }
+    <figcaption>
+        Residuals Histogram. Adapted from "Residual Plot Analysis”. 
+        Retrieved from [here](https://www.originlab.com/doc/origin-help/residual-plot-analysis).
+    </figcaption>
+</figure>