|
| 1 | +--- |
| 2 | +layout: post |
| 3 | +title: "[수치해석] 유한차분법 (Finite Difference Method)" |
| 4 | +date: 2022-3-10 22:00 |
| 5 | +categories: [Python, MathematicalProgramming] |
| 6 | +use_math: true |
| 7 | +comments: true |
| 8 | +--- |
| 9 | + |
| 10 | + |
| 11 | +## 유한차분을 이용한 미분값 근사 |
| 12 | + |
| 13 | +유한차분법 (Finite Difference Method, FDM)은 미분방정식을 수치적으로 풀이하는 방법이며, 도함수를 유한차분을 이용하여 근사하는 것이 핵심이다. 이번 포스팅 시리즈에서는 유한차분법을 이용하여 미분방정식을 수치적으로 풀이하는 방법에 대해 다뤄볼 예정이다. 먼저 smooth 함수 $u:\mathbb{R} \rightarrow \mathbb{R}$가 주어졌다고 하자. [smooth 함수](https://en.wikipedia.org/wiki/Smoothness)라고 하면 보통 원하는 횟수만큼 미분 가능한 함수를 말한다. 미분에 대해 이야기할 것이니 앞으로 미분가능한 함수만 고려하겠다는 의미다.<br><br> |
| 14 | + |
| 15 | + |
| 16 | +우리의 목표는 $u(x)$의 도함수 $u'(x)$를 계산하는 것이다. 물론, 중고등학교 때 배운 미분공식들을 사용하여 해석적으로 도함수를 계산할 수 있다. 하지만 여러 이유로 도함수를 해석적으로 계산하지 못할 때가 있다. 한 가지 상황을 예를 들자면, $u(x)$의 식이 주어지지 않고 특정 몇 개의 점에서 함수값만 알고 있을 수도 있다. 이때는 도함수를 해석적으로 계산하지 못하고 수치적으로 근사해야만 한다.<br><br> |
| 17 | + |
| 18 | +$x$에서의 도함수 $u'(x)$는 $x$와 $x$ 주변의 점을 이용해서 근사할 수 있다. 충분히 작은 양수 $h>0$에 대해서 $x$와 $x+h$에서의 함수값을 알 때, forward difference는 다음과 같이 미분값에 근사한다. |
| 19 | + |
| 20 | +$$D_{+}u(x):=\frac{u(x+h) - u(x)}{(x+h) - x}=\frac{u(x+h) - u(x)}{h}. \quad \quad (1)$$ |
| 21 | + |
| 22 | +<br> |
| 23 | + |
| 24 | +두 점 $x$와 $x-h$를 사용해서 미분값을 근사시킬 수도 있다. backward difference는 다음과 같이 미분값에 근사한다. |
| 25 | + |
| 26 | +$$D_{-}u(x):=\frac{u(x) - u(x-h)}{x - (x-h)}=\frac{u(x) - u(x-h)}{h}. \quad \quad (2)$$ |
| 27 | + |
| 28 | +<br> |
| 29 | + |
| 30 | +$u'(x)$를 구하는 것이 목표지만 굳이 $u(x)$를 쓰지 않고 $u(x-h)$와 $u(x+h)$를 사용해도 좋다. central difference는 다음과 같이 미분값에 근사한다. |
| 31 | + |
| 32 | +$$D_{0}u(x):=\frac{u(x+h) - u(x-h)}{(x+h) - (x-h)}=\frac{u(x+h) - u(x-h)}{2h}. \quad \quad (3)$$ |
| 33 | + |
| 34 | +<br> |
| 35 | + |
| 36 | +혹자는 함수값 2개만 사용하는 것이 아니라, 함수값 4개를 사용해서 미분값을 근사시킬 수도 있다. 예를 들어, 네 점 $x+h, x, x-h, x-2h$을 사용하여 미분값을 근사시킬 수 있다. |
| 37 | + |
| 38 | +$$D_{3}u(x):=\frac{1}{6h}\left[2u(x+h)+3u(x)-6u(x-h)+u(x-2h)\right]. \quad \quad (4)$$ |
| 39 | + |
| 40 | +<br> |
| 41 | + |
| 42 | +계수들이 어떻게 결정되는지는 잠시 후에 알아보자. |
| 43 | + |
| 44 | +<br> |
| 45 | + |
| 46 | +--- |
| 47 | + |
| 48 | + |
| 49 | + |
| 50 | +## 수치적 방법론들의 수렴률 / 정확도 |
| 51 | + |
| 52 | +위의 예시들에서 알 수 있는 것처럼, 미분값 $u(x)$에 근사하기 위해 다양한 조합의 함수값들을 사용할 수 있다. 일반적으로 많은 점들을 사용할 수록 실제 미분값과 근사값 사이의 오차가 빠르게 감소한다. 오차가 작은거면 작은거지 오차가 빠르게 감소한다는 표현은 무엇일까? 위의 예시들에서 $h$를 충분히 작은 양수라고만 소개하였다. 이 $h$ 값에 따라서 오차가 달라진다. 일반적으로 $h$가 작으면 작을수록 오차도 작아진다. 다시 돌아와서 "오차가 빠르게 감소한다"라는 것은 오차의 수렴률에 대한 이야기이다. 보통 빅오 표기(big O notation)를 사용해서 수치적 방법론들의 수렴률 (또는 정확성)을 나타낸다. |
| 53 | + |
| 54 | +<br> |
| 55 | + |
| 56 | +어떤 함수 $f(h), g(h)$에 대해서 $f(h)=\mathcal{O}(g(h))$ as $h \rightarrow 0$라는 것은 $f$가 $g$만큼 빠르게 감소한다는 것을 의미한다. 정확한 정의는 충분히 작은 모든 $h$에 대하여 |
| 57 | +$$\left| \frac{f(h)}{g(h)} \right| < C,$$ |
| 58 | + |
| 59 | +<br> |
| 60 | + |
| 61 | +인 상수 $C$를 찾을 수 있을 경우 $f(h)=\mathcal{O}(g(h))$ as $h \rightarrow 0$라고 한다. 예를 들어, $f(h)=\mathcal{O}(h^2)$의 의미는 $h$가 0으로 갈 때, $f$는 최소한 $h^2$이 0으로 가는 속도만큼 빠르게 0으로 간다는 것을 의미한다. 다시 돌아와서 식 $(1)$과 $(2)$는 $\mathcal{O}(h)$이고, 식 $(3)$은 $\mathcal{O}(h^2)$ 이며, 식 $(4)$는 $\mathcal{O}(h^3)$이다. 수렴률을 구하는 방법은 잠시 후에 알아보자.<br><br> |
| 62 | + |
| 63 | +그렇다고 무조건 많은 함수값을 사용하는 것이 좋은 것은 아니다. 오차는 줄어들 수 있겠지만 그만큼 많은 함수값 계산이 필요하기 때문에 수치적 풀이에 많은 시간이 소요될 수도 있다. 계산 속도와 오차 사이의 트레이드 오프 관계에서 적당히 좋은 방법론을 사용해야 할 것이다. |
| 64 | + |
| 65 | +<br> |
| 66 | + |
| 67 | +--- |
| 68 | + |
| 69 | +## [실습] |
| 70 | +$u(x)=\sin(x)$라고 할 때, $x=1$에서의 $u'(x)$ 값을 수치적으로 구해보자. 실제 미분값은 $\cos(1)$일 것이다. $h$ 값이 각각 $0.1, 0.05, 0.01, 0.005, 0.001$일 때 근사값을 구할 것이다. 마지막으로 실제 미분값에서 근사값을 빼줘서 오차의 크기를 출력해볼 것이다. |
| 71 | + |
| 72 | + |
| 73 | +```python |
| 74 | +import numpy as np |
| 75 | + |
| 76 | +def u(x): |
| 77 | + return np.sin(x) |
| 78 | + |
| 79 | +h_list = [1e-1, 5e-2, 1e-2, 5e-3, 1e-3] |
| 80 | +x = 1 |
| 81 | + |
| 82 | +results = [] |
| 83 | +for h in h_list: |
| 84 | + D_plus = (u(x + h) - u(x)) / h |
| 85 | + D_minus = (u(x) - u(x - h)) / h |
| 86 | + D_0 = (u(x + h) - u(x - h)) / 2 / h |
| 87 | + D_3 = (2 * u(x + h) + 3 * u(x) - 6 * u(x - h) + u(x - 2 * h)) / 6 / h |
| 88 | + |
| 89 | + results.append([D_plus, D_minus, D_0, D_3]) |
| 90 | + |
| 91 | +results = np.cos(1) - np.array(results) |
| 92 | +print(results) |
| 93 | +``` |
| 94 | + |
| 95 | + [[ 4.29385533e-02 -4.11384459e-02 9.00053698e-04 -6.82069338e-05] |
| 96 | + [ 2.12574901e-02 -2.08072945e-02 2.25097822e-04 -8.64914174e-06] |
| 97 | + [ 4.21632486e-03 -4.19831487e-03 9.00499341e-06 -6.99412992e-08] |
| 98 | + [ 2.10592434e-03 -2.10142182e-03 2.25125680e-06 -8.75402917e-09] |
| 99 | + [ 4.20825508e-04 -4.20645407e-04 9.00504502e-08 -6.99794667e-11]] |
| 100 | + |
| 101 | + |
| 102 | +<br> |
| 103 | + |
| 104 | +출력물의 열들은 각각 $D\_{+}, D\_{-}, D\_{0}, D\_{3}$을 나타내고, 행들은 $h$ 값을 나타낸다. 수치적으로 보는 것은 가시성이 좋지 않으니 오차를 시각화해보자. 오차 시각화는 보통 $\log (h)$에 따른 $log \left\| E(h) \right\|$를 시각화 한다. 그 이유는 위에서 본 수렴률과 상관 있다. 보통 오차의 수렴률을 $E(h)=\mathcal{O}(h^p)$와 같이 나타내는데, 빅오의 정의에 따라 $E(h) \approx Ch^p$이고 양변에 로그를 취해주면 다음과 같이 직선의 방정식 형태로 나타낼 수 있기 때문이다. 기울기가 order $p$이다. |
| 105 | + |
| 106 | +$$\log \left| E(h) \right| \approx \log \left| C \right| + p \log h$$ |
| 107 | + |
| 108 | + |
| 109 | +```python |
| 110 | +import matplotlib.pyplot as plt |
| 111 | +plt.rcParams['font.size'] = 14 |
| 112 | + |
| 113 | +results = np.abs(results) |
| 114 | + |
| 115 | +plt.figure(figsize=(6, 6)) |
| 116 | + |
| 117 | +plt.plot(np.log10(h_list), np.log10(results[:, 0]), 'o-', label='$D_{+}$') |
| 118 | +plt.plot(np.log10(h_list), np.log10(results[:, 1]), 'o-', label='$D_{-}$') |
| 119 | +plt.plot(np.log10(h_list), np.log10(results[:, 2]), 'o-', label='$D_{0}$') |
| 120 | +plt.plot(np.log10(h_list), np.log10(results[:, 3]), 'o-', label='$D_{3}$') |
| 121 | + |
| 122 | +plt.xticks(ticks=[-3, -2, -1], labels=['$10^{-3}$', '$10^{-2}$', '$10^{-1}$']) |
| 123 | +plt.yticks(ticks=[-2, -4, -6, -8, -10], labels=['$10^{-2}$', '$10^{-4}$', '$10^{-6}$', '$10^{-8}$', '$10^{-10}$']) |
| 124 | + |
| 125 | +plt.xlabel("$\log (h)$") |
| 126 | +plt.ylabel("$\log \mid E(h) \mid$") |
| 127 | + |
| 128 | +plt.legend() |
| 129 | +plt.show() |
| 130 | +``` |
| 131 | + |
| 132 | + |
| 133 | + |
| 134 | +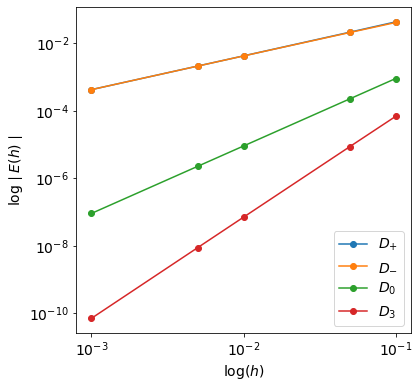 |
| 135 | + |
| 136 | + |
0 commit comments